No CrossRef data available.
Published online by Cambridge University Press: 29 November 2021
In this paper we study the small-scale equidistribution property of random waves whose coefficients are determined by an unfair coin. That is, the coefficients take value
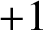 $+1$
with probability p and
$+1$
with probability p and
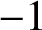 $-1$
with probability
$-1$
with probability
 $1-p$
. Random waves whose coefficients are associated with a fair coin are known to equidistribute down to the wavelength scale. We obtain explicit requirements on the deviation from the fair (
$1-p$
. Random waves whose coefficients are associated with a fair coin are known to equidistribute down to the wavelength scale. We obtain explicit requirements on the deviation from the fair (
 $p=0.5$
) coin to retain equidistribution.
$p=0.5$
) coin to retain equidistribution.
Communicated by Nathan Ross
The first author was supported by the University of Auckland’s Summer Scholar Scheme.