Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T17:53:24.906Z Has data issue: false hasContentIssue false
  • English
  • Français

SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES

Part of: Differential equations in the complex domain Zeta and $L$-functions: analytic theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  18 June 2018

STÉPHANE FISCHLER
STÉPHANE FISCHLER*
Affiliation:
Laboratoire de Mathématiques d’Orsay, Univ. Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we follow the approach of Bertrand–Beukers (and of Bertrand’s later work), based on differential Galois theory, to prove a very general version of Shidlovsky’s lemma that applies to Padé-approximation problems at several points, both at functional and numerical levels (that is, before and after evaluating at a specific point). This allows us to obtain a new proof of the Ball–Rivoal theorem on irrationality of infinitely many values of the Riemann zeta function at odd integers, inspired by the proof of the Siegel–Shidlovsky theorem on values of 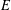$E$-functions: Shidlovsky’s lemma is used to replace Nesterenko’s linear independence criterion with Siegel’s, so that no lower bound is needed on the linear forms in zeta values. The same strategy provides a new proof, and a refinement, of Nishimoto’s theorem on values of 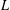$L$-functions of Dirichlet characters.

Keywords

irrationalityzeta valuesPadé approximationShidlovsky’s lemma

MSC classification

Primary: 11J72: Irrationality; linear independence over a field
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$ 34M03: Linear equations and systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 2 , October 2018 , pp. 145 - 172
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

André, Y., G-Functions and Geometry, Aspects of Mathematics, E13 (Vieweg, 1989).Google Scholar
Apéry, R., ‘Irrationalité de 𝜁(2) et 𝜁(3)’, in: Journées Arithmétiques (Luminy, 1978), Astérisque, 61 (Société Mathématique de France, 1979), 11–13.Google Scholar
Ball, K. M. and Rivoal, T., ‘Irrationalité d’une infinité de valeurs de la fonction zêta aux entiers impairs’, Invent. Math. 146(1) (2001), 193–207.Google Scholar
Bertrand, D., ‘Le théorème de Siegel–Shidlovsky revisité’, in: Number Theory, Analysis and Geometry: in Memory of Serge Lang (eds. Goldfeld, D. et al. ) (Springer, 2012), 51–67.Google Scholar
Bertrand, D. and Beukers, F., ‘Équations différentielles linéaires et majorations de multiplicités’, Ann. Sci. Éc. Norm. Supér. (4) 18(1) (1985), 181–192.Google Scholar
Beukers, F., ‘Padé-approximations in number theory’, in: Padé Approximation and its Applications (Amsterdam, 1980), Lecture Notes in Mathematics, 888 (Springer, 1981), 90–99.Google Scholar
Colmez, P., ‘Arithmétique de la fonction zêta’, in: Journées mathématiques X-UPS 2002 (éditions de l’école Polytechnique, 2003), 37–164.Google Scholar
Fel’dman, N. I. and Nesterenko, Yu. V., Number Theory IV, Transcendental Numbers, Encyclopaedia of Mathematical Sciences, 44 (eds. Parshin, A. N. and Shafarevich, I. R.) (Springer, 1998).Google Scholar
Fischler, S., ‘Irrationalité de valeurs de zêta (d’après Apéry, Rivoal, …)’, in: Sém. Bourbaki 2002/03, Astérisque, 294 (Société Mathématique de France, 2004), 27–62. exp. no. 910.Google Scholar
Fischler, S. and Rivoal, T., ‘Approximants de Padé et séries hypergéométriques équilibrées’, J. Math. Pures Appl. (9) 82(10) (2003), 1369–1394.Google Scholar
Galochkin, A. I., ‘Estimates for the number of zeros of certain functions with algebraic coefficients of Taylor series’, Mat. Zametki [Math. Notes] 61(6) (1997), 817–824 [687–692].Google Scholar
Habsieger, L., ‘Introduction to diophantine approximation’, manuscript.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, 2004).Google Scholar
Krattenthaler, C., Rivoal, T. and Zudilin, W., ‘Séries hypergéométriques basiques, q-analogues des valeurs de la fonction zêta et séries d’Eisenstein’, J. Inst. Math. Jussieu 5(1) (2006), 53–79.Google Scholar
Marcovecchio, R., ‘Linear independence of linear forms in polylogarithms’, Ann. Sc. Norm. Super. Pisa V(1) (2006), 1–11.Google Scholar
Matala-aho, T., ‘On Diophantine approximations of the solutions of q-functional equations’, Proc. Roy. Soc. Edinburgh Sect. A 132 (2002), 639–659.Google Scholar
Nash, M. H., ‘Special values of Hurwitz zeta functions and Dirichlet $L$ -functions’, PhD Thesis, University of Georgia, Athens, USA, 2004.Google Scholar
Neukirch, J., Algebraic Number Theory (Springer, 1999).Google Scholar
Nikishin, E. M., ‘On the irrationality of the values of the functions F (x, s)’, Mat. Sbornik [Math. USSR-Sb.] 109 [37](3) (1979), 410–417 [381–388].Google Scholar
Nishimoto, M., ‘On the linear independence of the special values of a Dirichlet series with periodic coefficients’, Preprint, 2011, arXiv:1102.3247 [math.NT].Google Scholar
Ramis, J. P., Séries Divergentes et Théories Asymptotiques, Panoramas et Synthèses, 21 (Soc. Math., France, Paris, 1993).Google Scholar
Rivoal, T., ‘La fonction zêta de Riemann prend une infinité de valeurs irrationnelles aux entiers impairs’, C. R. Acad. Sci. Paris Ser. I 331(4) (2000), 267–270.Google Scholar
Rivoal, T., ‘Indépendance linéaire des valeurs des polylogarithmes’, J. Théor. Nombres Bordeaux 15(2) (2003), 551–559.Google Scholar
Rivoal, T. and Zudilin, W., ‘Diophantine properties of numbers related to Catalan’s constant’, Math. Ann. 326(4) (2003), 705–721.Google Scholar
Shidlovsky, A. B., Transcendental Numbers, de Gruyter Studies in Mathematics, 12 (de Gruyter, Berlin, 1989).Google Scholar
Sorokin, V. N., ‘Hermite-Padé approximations for Nikishin systems and the irrationality of 𝜁(3)’, Uspekhi Mat. Nauk [Russian Math. Surveys] 49(2) (1994), 167–168 [176–177].Google Scholar
Sorokin, V. N., ‘Apéry’s theorem’, Vestnik Moskov. Univ. Ser. I Mat. Mekh. [Moscow Univ. Math. Bull.] 53(3) (1998), 48–53 [48–52].Google Scholar
Wechsung, G., ‘Functional equations of hyperlogarithms’, in: Structural Properties of Polylogarithms, Mathematics Surveys and Monographs, 37 (ed. Lewin, L.) (American Mathematical Society, 1991), 171–184.Google Scholar
Zudilin, W., ‘Lower bounds for polynomials in the values of certain entire functions’, Mat. Sbornik [Sb. Math.] 187(12) (1996), 57–86 [1791–1818].Google Scholar