Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-29T11:51:27.619Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequential Tests for Normal Markov Sequence

Published online by Cambridge University Press:  09 April 2009

R. M. Phatarfod
R. M. Phatarfod
Affiliation:
Monash UniversityClayton, Victoria
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This is a sequel to the author's (Phatarfod [9]) paper in which an analogue of Wald's Fundamental Identity (F.I.) for random variables defined on a Markov chain with a finite number of states was derived. From it the sampling properties of sequential tests of simple hypotheses about the parameters occurring in the transition probabilities were obtained. In this paper we consider the case of continuous Markovian variables. We restrict our attention to the practically important case of a Normal Markov sequence X0,X1,X2,… such that 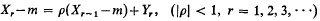the Yr being independent normal variables with mean zero and variance σ2.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 12 , Issue 4 , November 1971 , pp. 433 - 440
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Birkhoff, G., ‘Extensions of Jentzsch's theorem’, Trans. Amer. Math. Soc. 85 (1957), 219–227.Google Scholar
[2]Chung, K. L., Markov chains with stationary transition probabilities (Springer-Verlag, Berlin, 1960).CrossRefGoogle Scholar
[3]Cox, D. R., ‘Sequential tests for composite hypotheses’, Proc. Camb. Phil. Soc. 48 (1952), 290–299.CrossRefGoogle Scholar
[4]Daniels, H. E., ‘The approximate distribution of serial correlation coefficients’, Biometrika 43 (1956), 169–185.CrossRefGoogle Scholar
[5]Harris, T. E., The Theory of Branching Processes (Springer-Verlag, Berlin, 1963).CrossRefGoogle Scholar
[6]Jentzsch, R., ‘Über Integralgleichungen mit positivem Kern, J. Reine Angew, Math. 141 (1912), 235–244.CrossRefGoogle Scholar
[7]Karlin, S., ‘Positive Operators’, J. Math. Mech. 8 (1957), 907–938.Google Scholar
[8]Krein, M. G. and Rutman, M. A., ‘Linear operators leaving invariant a cone in a Banach space’, Amer. Math. Soc. Translation No. 26, 1950.Google Scholar
[9]Phatarfod, R. M., ‘Sequential analysis of dependent observations I’, Biometrika 52 (1965), 157–165.CrossRefGoogle Scholar
[10]Phatarfod, R. M., ‘A note on the cumulation sums of Markovian variables’, J. Aust. Math. Soc. 5 (1965), 285–287.CrossRefGoogle Scholar
[11]Vere-Jones, D., ‘Ergodic properties of non-negative matrices-I’, Pacific. J. Math. 22 (1967) 361–386.CrossRefGoogle Scholar
[12]Wald, A., Sequential Analysis (J. Wiley, New York, 1947).Google Scholar