We consider infinite sequences 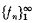of positive integers having exponential growth: 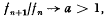and becoming ultimately periodic modulo each member of a rather sparse infinite set of integers. If sufficient, natural conditions are placed on the growth and periodicities of 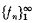, we find that a is an algebraic integer having all its algebraic conjugates within or on the unit circle, and fn has a special representation involving an. The result is a kind of dual to the theorem of Pisot (cf. Salem [2], p. 4, Theorem A).