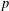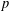Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beer, G.
and
Vanderwerff, J.
2015.
Structural Properties of Extended Normed Spaces.
Set-Valued and Variational Analysis,
Vol. 23,
Issue. 4,
p.
613.
Salas, David
and
Tapia-García, Sebastián
2016.
Extended seminorms and extended topological vector spaces.
Topology and its Applications,
Vol. 210,
Issue. ,
p.
317.
Kumar, Akshay
and
Jindal, Varun
2023.
Dual of an extended locally convex space.
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 2,
p.
127474.
Kumar, Akshay
and
Jindal, Varun
2023.
The finest locally convex topology of an extended locally convex space.
Topology and its Applications,
Vol. 326,
Issue. ,
p.
108396.
Kumar, Akshay
and
Jindal, Varun
2024.
Extended locally convex spaces: Barreledness, equicontinuity and Banach-Steinhaus theorem.
Topology and its Applications,
Vol. 348,
Issue. ,
p.
108890.
Kumar, Akshay
and
Jindal, Varun
2024.
Reflexive extended locally convex spaces.
Journal of Mathematical Analysis and Applications,
Vol. 540,
Issue. 1,
p.
128559.