Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T13:58:00.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Semigroup structures for families of functions, III

-Semigroups

Published online by Cambridge University Press:  09 April 2009

Kenneth D. Magill Jr
Kenneth D. Magill Jr
Affiliation:
State University of New York at Buffalo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

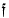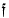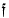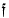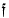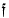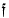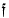Let Fx and Fy denote families of subsets of the nonempty sets X and Y respectively and let be a function mapping Y onto X with the property that [H] ∈ Fx for each H∈Fy. Then the family l of all functions mapping X into Y such that [H] ∈Fy for each H ∈Fx is a semigroup if the product g of two such functions and g is defined by g = o 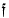o g (i.e., (Fg)(x) = 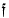(f(g(x))) for each x in X). With some restrictions on the families Fx and Fy and the function 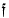, these are the semigroups mentioned in the title and are the objects of investigation in this paper. The restrictions on fxfy and 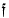are sufficiently mild so that the semigroups considered here include such semigroups of functions on topological spaces as semi- groups of closed functions, semigroups of connected functions, etc.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 7 , Issue 4 , November 1967 , pp. 524 - 538
Copyright
Copyright © Australian Mathematical Society 1967

References

[1]Birkhoff, G., ‘Sobre los grupos de automorfismos’, Rev. Union mat. Argent. 11 (1945), 155–157.Google Scholar
[2]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Mathematical Surveys, Number 7 (Amer. Math. Soc., 1961).Google Scholar
[3]de Groot, J., ‘Groups represented by homeomorphism groups, I’, Math. Annalen 138 (1959), 80–102.CrossRefGoogle Scholar
[4]Kelley, J. L., General Topology (Van Nostrand, Princeton, 1955).Google Scholar
[5]Kuratowski, C., Topologie II (Warsaw, 1950).Google Scholar
[6]Ljapin, E. S., Semigroups, Vol. 3, Translations of Mathematical Monographs (Amer. Math. Soc., 1963).CrossRefGoogle Scholar
[7]Magill, K. D. Jr, ‘Semigroups of functions on topological spaces’, Proc. London Math. Soc. (3) 16 (1966), 507–18.CrossRefGoogle Scholar
[8]Magill, K. D. Jr, ‘Semigroup structures for families of functions, I; Some homomorphism theorems’, Journ. Australian Math. Soc. 7 (1967), 81–94.CrossRefGoogle Scholar
[9]Magill, K. D. Jr, ‘Semigroup structures for families of functions, II; Continuous functions’, Journ. Australian Math. Soc. 7 (1967), 95–107.CrossRefGoogle Scholar
[10]Pervin, W. J. and Levine, N., ‘Connected mappings of Hausdorff spaces’, Proc. Amer. Math. Soc., 9 (1958), 488–96.CrossRefGoogle Scholar
[11]Vitanza, M. L., ‘Mappings of semigroups associated with ordered pairs’, Amer. Math. Monthly 73 (1966), 1078–1082.CrossRefGoogle Scholar