Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Magill, Kenneth D.
1967.
Semigroup structures for families of functions, III.
Journal of the Australian Mathematical Society,
Vol. 7,
Issue. 4,
p.
524.
Magill, K. D.
1975.
A survey of semigroups of continuous selfmaps.
Semigroup Forum,
Vol. 11,
Issue. 1,
p.
189.
Symons, J. S. V.
1975.
On a generalization of the transformation semigroup.
Journal of the Australian Mathematical Society,
Vol. 19,
Issue. 1,
p.
47.
1977.
Near-Rings - The Theory and its Applications.
Vol. 23,
Issue. ,
p.
437.
Magill, K. D.
and
Subbiah, S.
1978.
Green's relations for regular elements of sandwich semigroups, II; semigroups of continuous functions.
Journal of the Australian Mathematical Society,
Vol. 25,
Issue. 1,
p.
45.
Magill, K. D.
1987.
Automorphism groups of sandwich semigroups.
Mathematika,
Vol. 34,
Issue. 1,
p.
19.
Fuchs, Peter
1990.
On the structure of ideals in sandwich near-rings.
Results in Mathematics,
Vol. 17,
Issue. 3-4,
p.
256.
Vechtomov, E. M.
1991.
Specification of topological spaces by algebraic systems of continuous functions.
Journal of Soviet Mathematics,
Vol. 53,
Issue. 2,
p.
123.
Veldsman, Stefan
1992.
On equiprime near-rings.
Communications in Algebra,
Vol. 20,
Issue. 9,
p.
2569.
Wasanawichit, Amorn
and
Kemprasit, Yupaporn
2002.
Dense subsemigroups of generalised transformation semigroups.
Journal of the Australian Mathematical Society,
Vol. 73,
Issue. 3,
p.
433.
Dolinka, Igor
Đurđev, Ivana
East, James
Honyam, Preeyanuch
Sangkhanan, Kritsada
Sanwong, Jintana
and
Sommanee, Worachead
2018.
Sandwich semigroups in locally small categories I: foundations.
Algebra universalis,
Vol. 79,
Issue. 3,
Djurdjev-Brkovic, Ivana
2022.
Classification of variants of partial Brauer monoids.
Publications de l'Institut Mathematique,
Vol. 111,
Issue. 125,
p.
1.


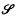 be a family of functions with domains contained in a set
be a family of functions with domains contained in a set 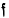 be a function with domain
be a function with domain 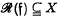 with the property
with the property 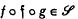 for each pair of elements ƒ and
for each pair of elements ƒ and 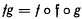 .
.