Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Magill, Kenneth D.
1967.
Semigroup structures for families of functions, III.
Journal of the Australian Mathematical Society,
Vol. 7,
Issue. 4,
p.
524.
Yamamuro, Sadayuki
1969.
A Note on Semigroups of Mappings on Banach Spaces.
Journal of the Australian Mathematical Society,
Vol. 9,
Issue. 3-4,
p.
455.
Cezus, Frank A.
1974.
Pseudo-idempotents in semigroups of functions.
Journal of the Australian Mathematical Society,
Vol. 18,
Issue. 2,
p.
182.
Sullivan, R. P.
1975.
Automorphisms of transformation semigroups.
Journal of the Australian Mathematical Society,
Vol. 20,
Issue. 1,
p.
77.
Symons, J. S. V.
1975.
Embedding a semigroup of transformations.
Journal of the Australian Mathematical Society,
Vol. 20,
Issue. 2,
p.
222.
Sullivan, R. P.
1975.
Generalised partial transformation semigroups.
Journal of the Australian Mathematical Society,
Vol. 19,
Issue. 4,
p.
470.
Symons, J. S. V.
1975.
On a generalization of the transformation semigroup.
Journal of the Australian Mathematical Society,
Vol. 19,
Issue. 1,
p.
47.
Magill, K. D.
1987.
Automorphism groups of sandwich semigroups.
Mathematika,
Vol. 34,
Issue. 1,
p.
19.
Wasanawichit, Amorn
and
Kemprasit, Yupaporn
2002.
Dense subsemigroups of generalised transformation semigroups.
Journal of the Australian Mathematical Society,
Vol. 73,
Issue. 3,
p.
433.
Araújo, João
and
Konieczny, Janusz
2003.
Automorphism groups of centralizers of idempotents.
Journal of Algebra,
Vol. 269,
Issue. 1,
p.
227.
Araújo, João
and
Konieczny, Janusz
2007.
A method of finding automorphism groups of endomorphism monoids of relational systems.
Discrete Mathematics,
Vol. 307,
Issue. 13,
p.
1609.
ARAÚJO, JOÃO
and
KONIECZNY, JANUSZ
2009.
GENERAL THEOREMS ON AUTOMORPHISMS OF SEMIGROUPS AND THEIR APPLICATIONS.
Journal of the Australian Mathematical Society,
Vol. 87,
Issue. 01,
p.
1.
Araújo, J.
Bünau, P.V.
Mitchell, J.D.
and
Neunhöffer, M.
2010.
Computing automorphisms of semigroups.
Journal of Symbolic Computation,
Vol. 45,
Issue. 3,
p.
373.
Mendes-Gonçalves, Suzana
and
Sullivan, R. P.
2013.
REGULAR ELEMENTS AND GREEN'S RELATIONS IN GENERALIZED TRANSFORMATION SEMIGROUPS.
Asian-European Journal of Mathematics,
Vol. 06,
Issue. 01,
p.
1350006.
Gorbatkov, A. B.
2013.
Interassociativity on a free commutative semigroup.
Siberian Mathematical Journal,
Vol. 54,
Issue. 3,
p.
441.
Huisheng, Pei
and
Weina, Deng
2013.
Naturally Ordered Semigroups of Partial Transformations Preserving an Equivalence Relation.
Communications in Algebra,
Vol. 41,
Issue. 9,
p.
3308.
Dolinka, Igor
and
East, James
2015.
Variants of finite full transformation semigroups.
International Journal of Algebra and Computation,
Vol. 25,
Issue. 08,
p.
1187.
Araújo, João
Bentz, Wolfram
Dobson, Edward
Konieczny, Janusz
and
Morris, Joy
2018.
Automorphism Groups of Circulant Digraphs With Applications to Semigroup Theory.
Combinatorica,
Vol. 38,
Issue. 1,
p.
1.
Dolinka, Igor
Ɖurđev, Ivana
East, James
Honyam, Preeyanuch
Sangkhanan, Kritsada
Sanwong, Jintana
and
Sommanee, Worachead
2018.
Sandwich semigroups in locally small categories II: transformations.
Algebra universalis,
Vol. 79,
Issue. 3,
Dolinka, Igor
Đurđev, Ivana
East, James
Honyam, Preeyanuch
Sangkhanan, Kritsada
Sanwong, Jintana
and
Sommanee, Worachead
2018.
Sandwich semigroups in locally small categories I: foundations.
Algebra universalis,
Vol. 79,
Issue. 3,
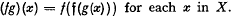 each x in X.
each x in X.