Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T23:05:18.205Z Has data issue: false hasContentIssue false
  • English
  • Français

The semigroup of endomorphisms of a Boolean ring

Published online by Cambridge University Press:  09 April 2009

Kenneth D. Magill Jr
Kenneth D. Magill Jr
Affiliation:
State University of New York at Buffalo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

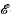The family (R) of all endomorphisms of a ring R is a semigroup under composition. It follows easily that if R and T are isomorphic rings, then 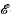(R) and 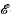(T) are isomorphic semigroups. We devote ourselves here to the converse question: ‘If 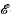(R) and 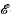(T) are isomorphic, must R and T be isomorphic?’ As one might expect, the answer is, in general, negative. For example, the ring of integers has precisely two endomorphisms – the zero endomorphism and the identity automorphism. Since the same is true of the ring of rational numbers, the two endomorphism semigroups are isomorphic while the rings themselves are certainly not.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 4 , November 1970 , pp. 411 - 416
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1 (Math. Surveys, No. 7, Amer. Math. Soc., 1961).Google Scholar
[2]Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, New York, 1960).CrossRefGoogle Scholar
[3]Howie, J. M., ‘The subsemigroup generated by the idempotents of a full transformation semigroup’, J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
[4]Magill, K. D. Jr,, ‘Another S-admissible class of spaces’, Proc. Amer. Math. Soc. 18 (1967), 295–298.Google Scholar
[5]Magill, K. D. Jr, and Glasenapp, J. A., ‘0-dimensional compactifications and Boolean rings’, J. Aust. Math. Soc. 8 (1968), 755–765.CrossRefGoogle Scholar
[6]Simons, G. F., Introduction to topology and modern analysis (McGraw-Hill, New York, 1963).Google Scholar