Hostname: page-component-f554764f5-qhdkw Total loading time: 0 Render date: 2025-04-13T12:18:46.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-polar double configurations in projective geometry: I. A general condition for self-polarity

Published online by Cambridge University Press:  09 April 2009

T. G. Room
T. G. Room
Affiliation:
University of Sydney, Sydney.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 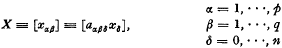be a p×q matrix of linear forms in the n+1 coordinates in a projective space Πn. Then points which satisfy the q equations in general span a space Πn-q, but will span a space Πn-q+1 if a set μ,={μβ of multipliers can be found such that Such a set μ can be found if and only if the equations have solutions.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 1 , February 1965 , pp. 65 - 68
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Room, T. G., Geometry of Determinantal Loci (Cambridge U.P., 1938).Google Scholar
[2]Coble, A. B., The double-Nn configuration, Duke Math. J. 9 (1942), 436.Google Scholar
[3]Baker, H. F., Principles of Geometry, Vol. III (Cambridge U.P., 1923).Google Scholar