Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T22:34:00.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Second nilpotent BFC groups

Published online by Cambridge University Press:  09 April 2009

Iain. M. Bride
Iain. M. Bride
Affiliation:
University of ManchesterInstitute of Science and TechnologyP.O. Box 88Manchester M60 1QD.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The BFC number of a group G is defined to be the least upper bound n of the cardinals of the conjugacy classes of G, provided this is finite, and we then say that G is n-BFC. It was shown by B. H. Neumann [2] that the derived group G′ of such a group is finite, and J. Wiegold [5] proved that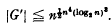.This bound was sharpened by I. D. Macdonald [1] to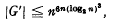, and P. M. Neumann has recently communicated the (unpublished) result that G′ ≦ nq(n) with q(n) a quadratic in log2w, an immense improvement on the above. J. A. H. Shepperd and J. Wiegold [4] improved the bound in two special cases, showing that if G is soluble, G′ ≦ np(n) with p(n) a quintic in Iog2n, and that if G is nilpotent of class 2, 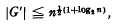, It is conjectured that for any n-BFC group G, 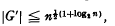, Wiegold [5] having shown that this bound is attained by certain nilpotent groups of class 2.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 1 , February 1970 , pp. 9 - 18
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Macdonald, I. D., ‘Some explicit bounds in groups with finite derived groups’, Proc. London Math. Soc. (3), 11 (1961) 23–56.CrossRefGoogle Scholar
[2]Neumann, B. H., ‘Groups with finite classes of conjugate elements’, Proc. London Math. Soc. 29 (1954) 236–248.CrossRefGoogle Scholar
[3]Scott, W. R., Group Theory (Prentice-Hall, 1964).Google Scholar
[4]Shepperd, J. A. H. and Wiegold, J., ‘Transitive permutation groups and groups with finite derived groups’, Math. Zeitschrift 81 (1963) 279–285.CrossRefGoogle Scholar
[5]Wiegold, J., ‘Groups with boundedly finite classes of conjugate elements’, Proc. Roy. Soc. A, 238 (1956) 389–401.Google Scholar