Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T04:10:17.946Z Has data issue: false hasContentIssue false
  • English
  • Français

Right invariant integrals on locally compact semigroups

Published online by Cambridge University Press:  09 April 2009

J. H. Michael
J. H. Michael
Affiliation:
University of Adelaide, South Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

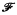An integral on a locally compact Hausdorff semigroup ς is a non-trivial, positive, linear functional μ on the space of continuous real-valued functions on ς with compact supports. If ς has the property: (A) for each pair of compact sets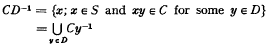 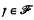C, D of S, the set is compact; then, whenever and a ∈ S, the function fa defined by is also in . An integral μ on a locally compact semigroup S with the property (A) is said to be right invariant if for all j ∈ and all a ∈ S.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 3 , August 1964 , pp. 273 - 286
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Birkhoff, G., A note on topological groups, Compositio Math. 3 (1936), 427–430.Google Scholar
[2]Halmos, P. R., Measure theory. Van Nostrand (1950).Google Scholar
[3]Kakutani, S., Über die Metrization der topologischen Gruppen, Proc. Imp. Acad. Jap. 12 (1936), 82–84.Google Scholar
[4]Kelley, J. L., General topology. Van Nostrand (1955).Google Scholar
[5]Montgomery, D. and Zippin, L., Topological transformation groups. Interscience tracts in pure and applied mathematics, Tract I (1955).Google Scholar
[6]Rosen, W. G., On invariant means over compact semigroups, Proc. Amer. Math. Soc. 7 (1956), 1076–1082.CrossRefGoogle Scholar
[7]Saks, S., Theory of the integral. Hafner (1937).Google Scholar