Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-22T23:13:55.943Z Has data issue: false hasContentIssue false
  • English
  • Français

A result for semi-regular continued fractions

Published online by Cambridge University Press:  09 April 2009

P. E. Blanksby
P. E. Blanksby
Affiliation:
Trinity CollegeCambridge
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If Φ is a real number with |Φ| ≧ 1, then a semiregular continuet fraction development of Φ is denoted by 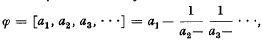where the ai are integers such that |ai| ≧ 2. The expansions arise geo-. metrically by considering the sequence of divided cells of two-dimensional grids (see [1]), and are described by the following algorithm: 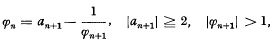for all n ≧ 0, taking Φ = Φ.0 Hence 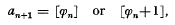where in this case the square brackets are used to signify the integer-part function. It follows that each irrational Φ has uncountably many such expansions, none of which has a constantly equal to 2 (or -2) for large n.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 1-2 , August 1969 , pp. 145 - 154
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Barnes, E. S. and Swinnerton-Dyer, H. P. F., The inhomogeneous minima of binary quadratic forms III, Acta Math. 92 (1954), 199–234.CrossRefGoogle Scholar
[2]Blanksby, P. E., A restricted inhomogeneous minimum for forms, to appear J. Aust. Math. Soc.Google Scholar
[3]Davenport, H., Indefinite binbary quadratic forms, and Euclid's algorithm in real quadratic fields, Proc. London Math. Soc. (2) 53 (1951), 65–82.CrossRefGoogle Scholar
[4]Hurwitz, A., Math. Werke II, 84–115.Google Scholar