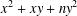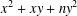Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cho, Bumkyu
2018.
On the number of representations of integers by quadratic forms with congruence conditions.
Journal of Mathematical Analysis and Applications,
Vol. 462,
Issue. 1,
p.
999.
Takeda, Wataru
2021.
On the finiteness of solutions for polynomial-factorial Diophantine equations.
Forum Mathematicum ,
Vol. 33,
Issue. 2,
p.
361.
Uchida, Naoki
2021.
Integers of the form $$ax^2+bxy+cy^2$$.
European Journal of Mathematics,
Vol. 7,
Issue. 3,
p.
1253.