Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T04:38:02.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on multipliers on certain function spaces on groups

Part of: Abstract harmonic analysis

Published online by Cambridge University Press:  09 April 2009

Hiroshi Yamaguchi
Hiroshi Yamaguchi
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be LCA group with an algebraically ordered dual Ĝ. Suppose also that the semigroup P of positive elements in Ĝ is not dense in Ĝ. Subspaces 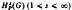(G) (1 < s < ∞) are defined analogous to the Hardy spaces on the circle group, and the question whether every multiplier from 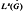into 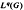can be extended to a multiplier from L3(G) into Lq(G) is investigated. If we suppose that s ≠ ∞, the it is shown that such an extension is possible if and only if (s, q) ∈ (1, ∞) × [1, ∞] ∪ {(1, ∞)}. (the negative result for (1, 1) was obtained in a previous paper.)

MSC classification

Secondary: 43A22: Homomorphisms and multipliers of function spaces on groups, semigroups, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 3 , October 1981 , pp. 276 - 288
Copyright
Copyright © Australian Mathematical Society 1981

References

Birtel, F. (1966), Function algebra, (Scott, Foresman and Company, Glenview, Illinois).Google Scholar
Doss, R. (1968), ‘On measures with small transforms’, Pacific J. Math. 26, 257–263.CrossRefGoogle Scholar
Doss, R. (1970), ‘On analytic contractions in Lp(G)’, Math. Z. 114, 59–65.CrossRefGoogle Scholar
Gaudry, G. I. (1968), ‘Hp multipliers and inequality of Hardy and Littlewood’, J. Austral. Math. Soc. 10, 23–32.CrossRefGoogle Scholar
Glicksberg, I. and Wik, I. (1971), ‘Multipliers of quotient of L1’, Pacific J. Math. 38, 619–624.CrossRefGoogle Scholar
Hewitt, E. and Ross, K. A. (1970), Abstract harmonic analysis II, (Springer-Verlag, Berlin-Heidelberg-New York).Google Scholar
Koshi, S. and Yamaguchi, H. (1979), ‘The F. and M. Riesz theorem and group structures’, Hokkaido Math. J. 8, 294–299.CrossRefGoogle Scholar
Larsen, R. (1971), Introduction to the theory of multipliers, (Springer-Verlag, Berlin-Heidelberg-New York).CrossRefGoogle Scholar
Otaki, H. (1977), ‘A relation between the F. and M. Riesz theorem and the structure of LCA groups’, Hokkaido Math. J. 6, 306–312.CrossRefGoogle Scholar
Power, S. (1977), ‘H∞ + AP is closed’, Proc. Amer. Math. Soc. 65, 73–76.Google Scholar
Rudin, W. (1962), Fourier analysis on groups, (Interscience, New York).Google Scholar
Yamaguchi, H. (1980), ‘Some multipliers on ’, J. Austral. Math. Soc. (Ser. A) 29, 52–60.CrossRefGoogle Scholar