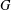Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lewis, Mark L.
2018.
Group Theory and Computation.
p.
141.
Li, Cai Heng
and
Wang, Lei
2019.
Finite REA-groups are solvable.
Journal of Algebra,
Vol. 522,
Issue. ,
p.
195.
Wang, Lei
2020.
On the automorphism groups of Frobenius groups.
Communications in Algebra,
Vol. 48,
Issue. 12,
p.
5330.
Wang, Lei
and
Qiao, Shou Hong
2021.
Frobenius REA-groups and their Cayley graphs.
Journal of Algebra and Its Applications,
Vol. 20,
Issue. 02,
p.
2150007.