Published online by Cambridge University Press: 09 April 2009
In this paper we begin with a short, direct proof that the Banach algebra B(l1) is not amenable. We continue by showing that various direct sums of matrix algebras are not amenable either, for example the direct sum of the finite dimensional algebras 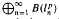 is no amenable for 1 ≤ p ≤ ∞, p ≠ 2. Our method of proof naturally involves free group algebras, (by which we mean certain subalgebras of B(X) for some space X with symmetric basis—not necessarily X = l2) and we introduce the notion of ‘relative amenability’ of these algebras.
is no amenable for 1 ≤ p ≤ ∞, p ≠ 2. Our method of proof naturally involves free group algebras, (by which we mean certain subalgebras of B(X) for some space X with symmetric basis—not necessarily X = l2) and we introduce the notion of ‘relative amenability’ of these algebras.