Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-11T13:53:57.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular Rees matrix semigroups and regular Dubreil-Jacotin semigroups

Part of: Semigroups

Published online by Cambridge University Press:  09 April 2009

D. B. Mcalister
D. B. Mcalister
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, Dekalb, Illinois 60115, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

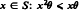A partially ordered semigroup S is said to be a Dubreil-Jacotin semigroup if there is an isotone homomorphism θ of S onto a partially ordered group such that {} has a greatest member. In this paper we investigate the structure of regular Dubreil-Jacotin semigroups in which the imposed partial order extends the natural partial order on the idempotents. The main tool used is a local structure theorem which is introduced in Section 2. This local structure theorem applies to many other contexts as well.

MSC classification

Secondary: 20M10: General structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 3 , October 1981 , pp. 325 - 336
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Allen, D. Jr, ‘A generalization of the Rees theorem to a class of regular semigroups’, Semigroup Forum 2 (1971), 321–331.CrossRefGoogle Scholar
[2]Blyth, T. S., ‘Dubreil-Jacotin inverse semigroups’, Proc. Roy. Soc. Edinburgh Sect. A 71 (1974), 345–360.Google Scholar
[3]Blyth, T. S., ‘The structure of certain ordered regular semigroups’, Proc. Roy. Soc. Edinburgh Sect. A 75 (1976), 235–257.CrossRefGoogle Scholar
[4]Blyth, T. S., ‘On a class of Dubreil-Jacotin semigroups and a construction of Yamada’, Proc. Roy. Soc. Edinburgh Sect. A 77 (1977), 145–150.CrossRefGoogle Scholar
[5]Blyth, T. S., ‘Perfect Dubreil-Jacotin semigroups’, Proc. Roy. Soc. Edinburgh Sect. A 78 (1977), 101–104.CrossRefGoogle Scholar
[6]Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
[7]McAlister, D. B., ‘Groups, semilattices and inverse semigroups, II’, Trans. Amer. Math. Soc. 196 (1974), 351–370.CrossRefGoogle Scholar
[8]McAlister, D. B. and Blyth, T. S., ‘Split orthodox semigroups’, J. Algebra 51 (1978), 491–525.CrossRefGoogle Scholar
[9]Nambooripad, K. S. S., ‘Structure of regular semigroups I’, Mem. Amer. Math. Soc. 22, Number 224 (1979).Google Scholar
[10]Nambooripad, K. S. S., ‘The natural partial order on a regular semigroup’, to appear.Google Scholar
[11]Pastijn, F. J., ‘Structure theorems for pseudo inverse semigroups’, Proceedings of a Symposium on Regular Semigroups, Northern Illinois University, 04 1979.Google Scholar