No CrossRef data available.
Article contents
RATIONAL 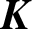 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 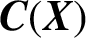 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS
Published online by Cambridge University Press: 10 May 2022
Abstract
We show that the properties of being rationally K-stable passes from the fibres of a continuous 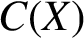 $C(X)$-algebra to the ambient algebra, under the assumption that the underlying space X is compact, metrizable, and of finite covering dimension. As an application, we show that a crossed product C*-algebra is (rationally) K-stable provided the underlying C*-algebra is (rationally) K-stable, and the action has finite Rokhlin dimension with commuting towers.
$C(X)$-algebra to the ambient algebra, under the assumption that the underlying space X is compact, metrizable, and of finite covering dimension. As an application, we show that a crossed product C*-algebra is (rationally) K-stable provided the underlying C*-algebra is (rationally) K-stable, and the action has finite Rokhlin dimension with commuting towers.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Robert Yuncken
The first named author is supported by UGC Junior Research Fellowship No. 1229, and the second named author was partially supported by the SERB (Grant No. MTR/2020/000385).



