No CrossRef data available.
Article contents
Rational approximation with series
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The Siegel conjecture on the rational approximation to algebraic numbers was proved a few years ago by K. F. Roth [1] with the following theorem: Let α be any algebraic number, not rational. If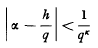
has an infinity of solutions in integers h and q (q > 0) tehn k ≤ 2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1961
References
[1]Roth, K. F., Rational approximations to algebraic numbers. Mathematika, Vol. 2, p. 1.CrossRefGoogle Scholar
[2]Gill, B. P., An analogue for algebraic functions of the Thue-Siegel theorem. Annals of Maths., Ser. 2, Vol. 31, p. 207.CrossRefGoogle Scholar
[3]Mahler, K., On a theorem of Liouville in fields of positive characteristic. Canadian Journal of Maths., Vol. 1, p. 397.CrossRefGoogle Scholar
You have
Access