Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:11:20.075Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMANUJAN SERIES WITH A SHIFT

Part of: Discontinuous groups and automorphic forms Other special functions

Published online by Cambridge University Press:  23 October 2018

JESÚS GUILLERA Open the ORCID record for JESÚS GUILLERA [Opens in a new window]
JESÚS GUILLERA*
Affiliation:
Department of Mathematics, University of Zaragoza, 50009 Zaragoza, Spain email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider an extension of the Ramanujan series with a variable $x$. If we let 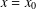$x=x_{0}$, we call the resulting series ‘Ramanujan series with the shift 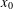$x_{0}$’. Then we relate these shifted series to some 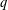$q$-series and solve the case of level 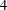$4$ with the shift 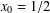$x_{0}=1/2$. Finally, we indicate a possible way towards proving some patterns observed by the author corresponding to the levels 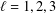$\ell =1,2,3$ and the shift 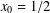$x_{0}=1/2$.

Keywords

Ramanujan series for 1/𝜋hypergeometric serieslattice sumsDirichlet L-valuesmodular forms

MSC classification

Primary: 33C20: Generalized hypergeometric series, $_pF_q$ 33C05: Classical hypergeometric functions, $_2F_1$
Secondary: 11F03: Modular and automorphic functions 33C75: Elliptic integrals as hypergeometric functions 33E05: Elliptic functions and integrals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 3 , December 2019 , pp. 367 - 380
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Borwein, J. M., Glasser, M. L., McPhedran, R. C., Wan, J. G. and Zucker, I. J., Lattice Sums Then and Now, Encyclopedia of Mathematics and its Applications, 150 (Cambridge University Press, Cambridge, 2013).Google Scholar
Chan, H. H., Chan, S. H. and Liu, Z., ‘Domb’s numbers and Ramanujan–Sato type series for 1/𝜋’, Adv. Math. 186 (2004), 396–410.Google Scholar
Glasser, M. L. and Zucker, I. J., ‘Lattice sums’, in: Theoretical Chemistry: Advances and Perspectives, Vol. 5 (eds. Eyring, H. and Henderson, D.) (Academic Press, New York, 1980), 67–139.Google Scholar
Guillera, J., ‘Series closely related to Ramanujan formulas for Pi’, unpublished paper (8 pages), 2003.Google Scholar
Guillera, J., ‘Series de Ramanujan: generalizaciones y conjeturas’, PhD Thesis, Universidad de Zaragoza, Spain, 2007.Google Scholar
Guillera, J., ‘A matrix form of Ramanujan-type series for 1/𝜋’, in: Gems in Experimental Mathematics, Contemporary Mathematics, 517 (eds. Amdeberhan, T., Medina, L. A. and Moll, V. H.) (American Mathematical Society, Washington, DC, 2010), 189–206.Google Scholar
Guillera, J., ‘WZ-proofs of ‘divergent’ Ramanujan-type series’, in: Waterloo Workshop in Computer Algebra in Memory of Herbert S. Wilf, Advances in Combinatorics (eds. Kotsireas, I. and Zima, E. V.) (Springer, Berlin–Heidelberg, 2013), 187–195.Google Scholar
Guillera, J. and Rogers, M., ‘Ramanujan series upside-down’, J. Aust. Math. Soc. 97 (2014), 78–106.Google Scholar
Petkovs̆ek, M., Wilf, H. S. and Zeilberger, D., A = B (A.K. Peters, Natick, MA, 1996).Google Scholar
Sloane, N. J. A., The On-Line Encyclopedia of Integer Sequences (OEIS), founded in 1964,https://oeis.org.Google Scholar
Yang, Y., ‘Apèry limits and special values of L-functions’, J. Math. Anal. Appl. 343 (2008), 492–513.Google Scholar