Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jankovics, Ronald
1975.
�ber Funktionen mit der Eigenschaft Re(e i? (f(z)/z-?))>0.
Mathematische Zeitschrift,
Vol. 143,
Issue. 3,
p.
235.
Li, Liulan
and
Ponnusamy, Saminathan
2013.
Injectivity of sections of univalent harmonic mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 89,
Issue. ,
p.
276.
Li, Liulan
and
Ponnusamy, Saminathan
2013.
Disk of convexity of sections of univalent harmonic functions.
Journal of Mathematical Analysis and Applications,
Vol. 408,
Issue. 2,
p.
589.
Ponnusamy, Saminathan
Sahoo, Swadesh Kumar
and
Yanagihara, Hiroshi
2014.
Radius of convexity of partial sums of functions in the close-to-convex family.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 95,
Issue. ,
p.
219.
Li, Liulan
and
Ponnusamy, Saminathan
2016.
Injectivity of sections of convex harmonic mappings and convolution theorems.
Czechoslovak Mathematical Journal,
Vol. 66,
Issue. 2,
p.
331.
Ghosh, Nirupam
and
Vasudevarao, A.
2019.
On a subclass of harmonic close-to-convex mappings.
Monatshefte für Mathematik,
Vol. 188,
Issue. 2,
p.
247.
Islam, Saeed
Khan, Muhammad Ghaffar
Ahmad, Bakhtiar
Arif, Muhammad
and
Chinram, Ronnason
2020.
Q-Extension of Starlike Functions Subordinated with a Trigonometric Sine Function.
Mathematics,
Vol. 8,
Issue. 10,
p.
1676.
Kazımoğlu, Sercan
and
Deniz, Erhan
2022.
Partial sums of the Rabotnov function.
Acta Universitatis Sapientiae, Mathematica,
Vol. 14,
Issue. 2,
p.
250.
Tang, Huo
Arif, Muhammad
Ullah, Khalil
Khan, Nazar
Haq, Mirajul
Khan, Bilal
and
Attiya, Adel A.
2022.
Starlikeness Associated with Tangent Hyperbolic Function.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.


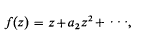
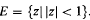 . G. Szegö [5] and Y. Miki [3] proved that if
. G. Szegö [5] and Y. Miki [3] proved that if