Published online by Cambridge University Press: 07 June 2019
We initiate a study of structural properties of the quotient algebra 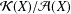 ${\mathcal{K}}(X)/{\mathcal{A}}(X)$ of the compact-by-approximable operators on Banach spaces
${\mathcal{K}}(X)/{\mathcal{A}}(X)$ of the compact-by-approximable operators on Banach spaces 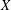 $X$ failing the approximation property. Our main results and examples include the following: (i) there is a linear isomorphic embedding from
$X$ failing the approximation property. Our main results and examples include the following: (i) there is a linear isomorphic embedding from 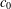 $c_{0}$ into
$c_{0}$ into 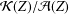 ${\mathcal{K}}(Z)/{\mathcal{A}}(Z)$, where
${\mathcal{K}}(Z)/{\mathcal{A}}(Z)$, where 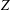 $Z$ belongs to the class of Banach spaces constructed by Willis that have the metric compact approximation property but fail the approximation property, (ii) there is a linear isomorphic embedding from a nonseparable space
$Z$ belongs to the class of Banach spaces constructed by Willis that have the metric compact approximation property but fail the approximation property, (ii) there is a linear isomorphic embedding from a nonseparable space 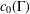 $c_{0}(\unicode[STIX]{x1D6E4})$ into
$c_{0}(\unicode[STIX]{x1D6E4})$ into 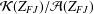 ${\mathcal{K}}(Z_{FJ})/{\mathcal{A}}(Z_{FJ})$, where
${\mathcal{K}}(Z_{FJ})/{\mathcal{A}}(Z_{FJ})$, where 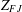 $Z_{FJ}$ is a universal compact factorisation space arising from the work of Johnson and Figiel.
$Z_{FJ}$ is a universal compact factorisation space arising from the work of Johnson and Figiel.
Communicated by A. Sims
H. Wirzenius gratefully acknowledges the financial support of The Swedish Cultural Foundation in Finland and the Magnus Ehrnrooth Foundation.