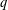Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T04:45:53.582Z Has data issue: false hasContentIssue false
  • English
  • Français

THE QUEER $q$-SCHUR SUPERALGEBRA

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  02 February 2018

JIE DU  and
JINKUI WAN
JIE DU
Affiliation:
School of Mathematics and Statistics, University of New South Wales, UNSW Sydney 2052, Australia email [email protected].
JINKUI WAN*
Affiliation:
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, 100081, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As a natural generalisation of 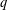$q$-Schur algebras associated with the Hecke algebra 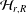${\mathcal{H}}_{r,R}$ (of the symmetric group), we introduce the queer 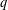$q$-Schur superalgebra associated with the Hecke–Clifford superalgebra 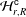${\mathcal{H}}_{r,R}^{\mathsf{c}}$, which, by definition, is the endomorphism algebra of the induced 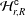${\mathcal{H}}_{r,R}^{\mathsf{c}}$-module from certain $q$-permutation modules over 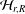${\mathcal{H}}_{r,R}$. We will describe certain integral bases for these superalgebras in terms of matrices and will establish the base-change property for them. We will also identify the queer $q$-Schur superalgebras with the quantum queer Schur superalgebras investigated in the context of quantum queer supergroups and provide a constructible classification of their simple polynomial representations over a certain extension of the field 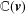$\mathbb{C}(\mathbf{v})$ of complex rational functions.

Keywords

Hecke–Clifford superalgebraq-Schur algebraqueer q-Schur superalgebraquantum queer supergroup

MSC classification

Primary: 20G43: Schur and $q$-Schur algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 3 , December 2018 , pp. 316 - 346
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Beilinson, A. A., Lusztig, G. and MacPherson, R., ‘A geometric setting for the quantum deformation of GL n ’, Duke Math. J. 61 (1990), 655–677.Google Scholar
Brundan, J. and Kleshchev, A., ‘Hecke–Clifford superalgebras, crystals of type A 2l (2) and modular branching rules for Ŝ n ’, Represent. Theory 5 (2001), 317–403.Google Scholar
Carter, R., Finite Groups of Lie Type: Conjugacy Classes and Complex Characters (John Wiley, New York, 1989).Google Scholar
Cheng, S.-J. and Wang, W., Dualities and Representations of Lie Superalgebras, Graduate Studies in Mathematics, 144 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Deng, B., Du, J. and Fu, Q., A Double Hall Algebra Approach to Affine Quantum Schur–Weyl Theory, LMS Lecture Note Series, 401 (Cambridge University Press, Cambridge, 2012).Google Scholar
Deng, B., Du, J., Parshall, B. and Wang, J., Finite Dimensional Algebras and Quantum Groups, Mathematical Surveys and Monographs, 150 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Dipper, R. and James, G., ‘Representations of Hecke algebras of general linear groups’, Proc. Lond. Math. Soc. (3) 52 (1986), 20–52.Google Scholar
Dipper, R. and James, G., ‘The q-Schur algebra’, Proc. Lond. Math. Soc. (3) 3 (1989), 23–50.Google Scholar
Du, J., ‘The modular representation theory of q-Schur algebras’, Trans. Amer. Math. Soc. 329 (1992), 253–271.Google Scholar
Du, J. and Gu, H., ‘A realisation of the quantum supergroup U(gl m|n )’, J. Algebra 404 (2014), 60–99.Google Scholar
Du, J., Gu, H. and Wang, J.-P., ‘Irreducible representations of q-Schur superalgebras at a root of unity’, J. Pure Appl. Algebra 218 (2014), 2012–2059.Google Scholar
Du, J. and Rui, H., ‘Based algebras and standard bases for quasi-hereditary algebras’, Trans. Amer. Math. Soc. 350 (1998), 3207–3235.Google Scholar
Du, J. and Rui, H., ‘Quantum Schur superalgebras and Kazhdan–Lusztig combinatorics’, J. Pure Appl. Algebra 215 (2011), 2715–2737.Google Scholar
Du, J. and Wan, J., ‘Presenting queer Schur superalgebras’, Int. Math. Res. Not. IMRN 2015(8) (2015), 2210–2272.Google Scholar
El Turkey, H. and Kujawa, J., ‘Presenting Schur superalgebras’, Pacific J. Math. 262 (2013), 285–316.Google Scholar
Graham, J. J. and Lehrer, G. I., ‘Cellular algebras’, Invent. Math. 123 (1996), 1–34.Google Scholar
Grantcharov, D., Jung, J., Kang, S.-J., Kashiwara, M. and Kim, M., ‘Crystal bases for the quantum queer superalgebra’, J. Eur. Math. Soc. (JEMS) 17 (2015), 1593–1627.Google Scholar
Green, J. A., Polynomial Representations of GL n , 2nd edn, Lecture Notes in Mathematics, 830 (Springer, Berlin, 2007), with an appendix on Schensted correspondence and Littelmann paths by K. Erdmann, J. A. Green and M. Schocker.Google Scholar
Jimbo, M., ‘A q-analogue of U (gl (N + 1)), Hecke algebras, and the Yang–Baxter equation’, Lett. Math. Phys. 11 (1986), 247–252.Google Scholar
Jones, A. and Nazarov, M., ‘Affine Sergeev algebra and q-analogues of the Young symmetrizers for projective representations of the symmetric group’, Proc. Lond. Math. Soc. (3) 78 (1999), 481–512.Google Scholar
Józefiak, T., A Class of Projective Representations of Hyperoctahedral Groups and Schur Q-functions, Topics in Algebra, Banach Center Publications, 26, Part 2 (PWN-Polish Scientific, Warsaw, 1990), 317–326.Google Scholar
Kleshchev, A., Linear and Projective Representations of Symmetric Groups, Cambridge Tracts in Mathematics, 136 (Cambridge University Press, Cambridge, 2005).Google Scholar
Mitsuhashi, H., ‘Schur–Weyl reciprocity between the quantum superalgebra and the Iwahori–Hecke algebra’, Algebr. Represent. Theory 9 (2006), 309–322.Google Scholar
Mori, M., ‘A cellular approach to the Hecke–Clifford superalgebra’, Preprint, 2014, arXiv:1401.1722, 80 pages.Google Scholar
Olshanski, G. I., ‘Quantized universal enveloping superalgebra of type Q and a super-extension of the Hecke algebra’, Lett. Math. Phys. 24 (1992), 93–102.Google Scholar
Sergeev, A., ‘Tensor algebra of the identity representation as a module over the Lie superalgebras GL(n, m) and Q (n)’, Math. USSR Sb. 51 (1985), 419–427.Google Scholar
Wan, J. and Wang, W., ‘Frobenius character formula and spin generic degrees for Hecke–Clifford algebra’, Proc. Lond. Math. Soc. (3) 106 (2013), 287–317.Google Scholar