Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-05-01T18:48:46.936Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic Diophantine equations and two generator Möbius groups

Published online by Cambridge University Press:  09 April 2009

Eng-Chye Tan  and
Ser-Peow Tan
Ser-Peow Tan
Affiliation:
Department of Mathematics Faculty of Science National University of Singapore 10 Kent Ridge Crescent Singapore 0511 e-mail: [email protected] and [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the set of rational μ in (−2, 2) for which the group Gu generated by is not free by using quadratic Diophantine equations of the form ax2 −by2 = ±1. We give a new set of accumulation points for rational values of μ in (−2, 2) for which Gμ is not free, thereby extending the results of Beardon where he showed that 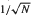are accumulation points, where N is an integer which is not a perfect square. In particular, we exhibit an infinite set of accumulation points for μ between 1 and 2 including the point 1.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 61 , Issue 3 , December 1996 , pp. 360 - 368
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Beardon, A., The geometry of discrete groups (Springer, New York, 1983).Google Scholar
[2]Beardon, A., ‘Pell's equation and two generator free Möbius groups’, Bull. London. Math. Soc. 25 (1993), 527–532.Google Scholar
[3]Chang, B., Jennings, S. A. and Ree, R., ‘On certain pairs of matrices which generate free groups’, Canad. J. Math. 10 (1958), 279–284.Google Scholar
[4]Flath, D. E., Introduction to number theory (Wiley, New York, 1989).Google Scholar
[5]Lyndon, R. C., and Ullman, J. L., ‘Groups generated by two linear parabolic transformations’, Canad. J. Math. 21 (1969), 1388–1403.Google Scholar