Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T13:47:30.849Z Has data issue: false hasContentIssue false
  • English
  • Français

PROFINITE GROUPS WITH FINITE VIRTUAL LENGTH

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  18 July 2013

NORBERTO GAVIOLI ,
VALERIO MONTI  and
CARLO MARIA SCOPPOLA
NORBERTO GAVIOLI
Affiliation:
Dipartimento di Ingegneria e, Scienze dell’Informazione e Matematica, Università degli Studi dell’Aquila, via Vetoio, 1, I-67010 Coppito (L’Aquila) AQ, Italy email [email protected]
VALERIO MONTI
Affiliation:
Dipartimento di Scienza, e Alta Tecnologia, Università degli Studi dell’Insubria, via Valleggio, 11, I-22100 Como, Italy email [email protected]
CARLO MARIA SCOPPOLA*
Affiliation:
Dipartimento di Ingegneria e, Scienze dell’Informazione e Matematica, Università degli Studi dell’Aquila, via Vetoio, 1, I-67010 Coppito (L’Aquila) AQ, Italy email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we introduce the notion of finite virtual length for profinite groups (that is, every series has a bounded number of infinite factors) and we prove a Jordan–Hölder type theorem for profinite groups with finite virtual length. More structural results are provided in the pronilpotent and 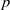$p$-adic analytic cases.

Keywords

profinite groups with operatorsJordan–Hölder theorempro-p groups

MSC classification

Secondary: 20E18: Limits, profinite groups 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 343 - 355
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Barnea, Y., Gavioli, N., Jaikin-Zapirain, A., Monti, V. and Scoppola, C. M., ‘Pro-p groups with few normal subgroups’, J. Algebra (2) 321 (2009), 429–449.CrossRefGoogle Scholar
Bartholdi, L., Grigorchuk, R. I. and Šunić, Z., ‘Branch groups’, in: Handbook of Algebra, Vol. 3 (North-Holland, Amsterdam, 2003), 989–1112.CrossRefGoogle Scholar
Bourbaki, N., Algebra I. Ch. 1–3, Elements of Mathematics (Berlin) (Springer, Berlin, 1998), translated from the French, reprint of the 1989 English translation.Google Scholar
Bourbaki, N., General Topology. Ch. 1–4, Elements of Mathematics (Berlin) (Springer, Berlin, 1998), translated from the French, reprint of the 1989 English translation.Google Scholar
Dixon, J. D. and du Sautoy, M. P. F., ‘Avinoam Mann and Dan Segal’, in: Analytic pro-p Groups, 2nd edn, Cambridge Studies in Advanced Mathematics, 61 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Grigorchuk, R. I., ‘Just infinite branch groups’, in: New Horizons in pro-p Groups (eds. du Sautoy, et al. ) (Birkhäuser, Boston, MA, 2000), 121–179.CrossRefGoogle Scholar
Leedham-Green, C. R. and McKay, S., The Structure of Groups of Prime Power Order, London Mathematical Society Monographs, New Series, 27 (Oxford University Press, Oxford, 2002).CrossRefGoogle Scholar
Nikolov, N. and Segal, D., ‘On finitely generated profinite groups. I. Strong completeness and uniform bounds’, Ann. of Math. (2) 165 (1) (2007), 171–238.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P., Profinite Groups, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge (Results in Mathematics and Related Areas, 3rd Series). A Series of Modern Surveys in Mathematics, 40 (Springer-Verlag, Berlin, 2010).CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups, 2nd edn, Graduate Texts in Mathematics, 80 (Springer, New York, 1996).CrossRefGoogle Scholar
Wilson, J. S., ‘On just infinite abstract and profinite groups’, in: New Horizons in pro-p Groups (eds. du Sautoy, et al. ) (Birkhäuser, Boston, MA, 2000), 181–203.CrossRefGoogle Scholar
Wilson, J. S., ‘Large hereditarily just infinite groups’, J. Algebra (2) 324 (2010), 248–255.CrossRefGoogle Scholar