Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T08:56:02.307Z Has data issue: false hasContentIssue false
  • English
  • Français

A problem of expressibility in some amalgamated products of groups

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  09 April 2009

Valerii Faiziev
Valerii Faiziev
Affiliation:
Tver Agricultural Academy Tver Russia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be a subset of a group G such that S−1 = S. Denote by gr (S) the subgroup of G generated by S, and by ls(g) the length of an element g ∈ gr(S) relative to the set S. Suppose that V is a finite subset of a free group F of countable rank such that the verbal subgroup V (F) is a proper subgroup of F. For an arbitrary group G, denote by 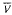(G) the set of values in G of all the words from the set V. In the present paper, for amalgamated products G = A *HB such that A ≠ H and the number of double cosets of B by H is at least three, the infiniteness of the set {ls(g) | g ∈ gr(S)}, where S = 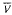(G) ∪ 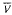(G)−1, is estabilished.

Keywords

Groupverbal subgroupthe width of verbal subgroup

MSC classification

Secondary: 20E06: Free products, free products with amalgamation, Higman-Neumann-Neumann extensions, and generalizations 20F22: Other classes of groups defined by subgroup chains
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 71 , Issue 1 , August 2001 , pp. 105 - 115
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Adjan, S. I. and Mennicke, J., ‘On bounded generation of SL(n, Z)’, Internat. J. Algebra Comput. 2 (1992), 357–355.Google Scholar
[2]Bardakov, V. G., ‘To the theory of braid groups’, Mat. Sb. 183 (1992), 3–43.Google Scholar
[3]Ellers, E. W., ‘Products of transvections in one conjugacy class in the symplectic group over GF(3)’, Linear Algebra Appl. 202 (1994), 1–23.CrossRefGoogle Scholar
[4]Faiziev, V. A., ‘Pseudocharacters on semidirect product of semigroups’, Mat. Zametki 53 (1993), 132–139.Google Scholar
[5]Faiziev, V. A., ‘Pseudocharacters on free semigroups’, Russian J. Math. Phys. 5 (1995), 191–206.Google Scholar
[6]Griffiths, H. B., ‘A note on commutators in free products’, Proc. Cambridge Phil. Soc. 50 (1954), 178–188.CrossRefGoogle Scholar
[7]Newnan, M., ‘Unimodular commutators’, Proc. Amer. Math. Soc. 101 (1987), 605–609.CrossRefGoogle Scholar
[8]Rhemtulla, A. H., ‘A problem of expressibility in free products’, Proc. Cambridge Phil. Soc. 64 (1968), 573–584.CrossRefGoogle Scholar
[9]Rhemtulla, A. H., ‘Commutators of certain finitely generated solvable groups’, Canad. J. Math. 64 (1969), 1160–1164.CrossRefGoogle Scholar