Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T12:45:17.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive linear operators and summability

Published online by Cambridge University Press:  09 April 2009

J. P. King  and
J. J. Swetits
J. P. King
Affiliation:
Lehigh University
J. J. Swetits
Affiliation:
Lafayette College
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

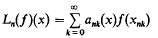Let {Ln} be a sequence of positive linear operators defined on C[a, b] of the form where xnk ∈ [a, b] for each k = 0, 1,…, n = 1, 2,…. The convergence properties of the sequences {Ln(f)} to for each f ∈ C[a, b] have been the object of much recent research (see e.g. [4], [8], [11], [13]). In many cases positive linear operators of the form (1) give rise to interesting summability matrices A = (ank(x)) and vice- versa.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 3 , August 1970 , pp. 281 - 290
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Agnew, R. P., ‘Euler Transformations’, Amer. J. Math. 66 (1944), 318–338.CrossRefGoogle Scholar
[2]Boehme, T. K. and Powell, R. E., ‘Positive Linear Operators Generated by Analytic Functions’, Siam J. Appl. Math., 16 (1968), 510–519.Google Scholar
[3]Cheney, E. W., Introduction to Approximation Theory (McGraw-Hill, 1966).Google Scholar
[4]Cheney, E. W. and Sharma, A., ‘Bernstein power series’, Can. J. Math. 16 (1964), 241–252.Google Scholar
[5]Cowling, V. F., ‘Summability and analytic continuation’, Proc. Amer. Math. Soc. 1 (1950), 536–542.CrossRefGoogle Scholar
[6]Jakimovski, A., ‘A generalization of the Lototsky method of summability’, Michigan Math. J. 6 (1959), 277–290.CrossRefGoogle Scholar
[7]King, J. P., ‘Almost summable sequences’, Proc. Amer. Math. Soc. 17 (1966), 1219–1225.CrossRefGoogle Scholar
[8]King, J. P., ‘The Lototsky transform and Bernstein Polynomials’, Can. J. Math. 18 (1966), 89–91.CrossRefGoogle Scholar
[9]Korovkin, P., Linear operators and approximation theory (translated from the Russian edition of 1959, Delhi, 1960).Google Scholar
[10]Lorentz, G. G., ‘A contribution to the theory of divergent sequences’, Acta. Math. 80 (1948), 167–190.Google Scholar
[11]Meyer-Konig, W. and Zeller, K., ‘Bernsteinsche Potenzreihen’, Studia Math. 19 (1960), 89–94.Google Scholar
[12]Wilansky, A., Functional Anatysis (Blaisdell, 1964).Google Scholar
[13]Bohman, H., ‘On approximation of continuous and of analytic functions’, Ark. Mat. 2 (1952) 43–56.Google Scholar