Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Móricz, F.
1989.
Walsh-Fourier series with coefficients of generalized bounded variation.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 47,
Issue. 3,
p.
458.
Lubinsky, D. S.
and
M�ricz, F.
1993.
Pointwise convergence of Fourier transforms.
Archiv der Mathematik,
Vol. 61,
Issue. 1,
p.
82.
Chen, Chang-Pao
and
Lin, Chin-Cheng
1995.
Almost everywhere convergence of Fourier integrals.
Archiv der Mathematik,
Vol. 64,
Issue. 4,
p.
333.
Chen, Chang-Pao
and
Wu, Ching-Tang
1998.
Double Walsh series with coefficients of bounded variation of higher order.
Transactions of the American Mathematical Society,
Vol. 350,
Issue. 1,
p.
395.


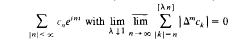 for some nonnegative integer
for some nonnegative integer 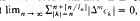 , where {
, where {