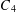 $C_{4}$
$C_{4}$Published online by Cambridge University Press: 09 October 2019
A Heron triangle is a triangle that has three rational sides 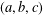 $(a,b,c)$ and a rational area, whereas a perfect triangle is a Heron triangle that has three rational medians
$(a,b,c)$ and a rational area, whereas a perfect triangle is a Heron triangle that has three rational medians 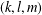 $(k,l,m)$. Finding a perfect triangle was stated as an open problem by Richard Guy [Unsolved Problems in Number Theory (Springer, New York, 1981)]. Heron triangles with two rational medians are parametrized by the eight curves
$(k,l,m)$. Finding a perfect triangle was stated as an open problem by Richard Guy [Unsolved Problems in Number Theory (Springer, New York, 1981)]. Heron triangles with two rational medians are parametrized by the eight curves  $C_{1},\ldots ,C_{8}$ mentioned in Buchholz and Rathbun [‘An infinite set of heron triangles with two rational medians’, Amer. Math. Monthly 104(2) (1997), 106–115; ‘Heron triangles and elliptic curves’, Bull. Aust. Math.Soc. 58 (1998), 411–421] and Bácskái et al. [Symmetries of triangles with two rational medians, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.65.6533, 2003]. In this paper, we reveal results on the curve
$C_{1},\ldots ,C_{8}$ mentioned in Buchholz and Rathbun [‘An infinite set of heron triangles with two rational medians’, Amer. Math. Monthly 104(2) (1997), 106–115; ‘Heron triangles and elliptic curves’, Bull. Aust. Math.Soc. 58 (1998), 411–421] and Bácskái et al. [Symmetries of triangles with two rational medians, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.65.6533, 2003]. In this paper, we reveal results on the curve 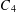 $C_{4}$ which has the property of satisfying conditions such that six of seven parameters given by three sides, two medians and area are rational. Our aim is to perform an extensive search to prove the nonexistence of a perfect triangle arising from this curve.
$C_{4}$ which has the property of satisfying conditions such that six of seven parameters given by three sides, two medians and area are rational. Our aim is to perform an extensive search to prove the nonexistence of a perfect triangle arising from this curve.