Article contents
Oscillatory and asymptotic properties of homogeneous and nonhomogeneous delay differential equations of even order
Published online by Cambridge University Press: 09 April 2009
Abstract
In this paper we consider the (non)oscillation properties of two general nonhomogeneous nonlinear delay differential equations of order 2n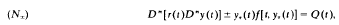 using as background and motivation the techniques previously applied to the associated homogeneous delay differential equations H+ and H−. The equations N+ and N− are each reduced to homogeneous form by the introduction of transformations u(t) = y(t) – R(t) and v(t) = R(t) — y(t), where R(t) is a solution of the associated nonhomogeneous differential equation (N). We first extend certain results for the equation H+ and then develop a classification of the positive solutions of equation H−. Using this classification and the one developed by Terry (1974) for H+ we develop a natural classification of the positive solutions of N+ and N− according to the sign properties of the derivatives of u(t) and v(t). For each choice of R(t), it is seen that there are 2n + 1 types of positive solutions of N+or N–. An intermediate Riccati transformation is employed to obtain integral criteriafor the nonexistence of some of these solutions. Analysis of the Taylor remainder results in sufficient conditions for the nonexistence of other such solutions.
using as background and motivation the techniques previously applied to the associated homogeneous delay differential equations H+ and H−. The equations N+ and N− are each reduced to homogeneous form by the introduction of transformations u(t) = y(t) – R(t) and v(t) = R(t) — y(t), where R(t) is a solution of the associated nonhomogeneous differential equation (N). We first extend certain results for the equation H+ and then develop a classification of the positive solutions of equation H−. Using this classification and the one developed by Terry (1974) for H+ we develop a natural classification of the positive solutions of N+ and N− according to the sign properties of the derivatives of u(t) and v(t). For each choice of R(t), it is seen that there are 2n + 1 types of positive solutions of N+or N–. An intermediate Riccati transformation is employed to obtain integral criteriafor the nonexistence of some of these solutions. Analysis of the Taylor remainder results in sufficient conditions for the nonexistence of other such solutions.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 22 , Issue 3 , November 1976 , pp. 282 - 304
- Copyright
- Copyright © Australian Mathematical Society 1976
References
- 3
- Cited by


