Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T12:26:27.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillations of higher order neutral differential equations

Part of: Functional-differential and differential-difference equations Qualitative theory

Published online by Cambridge University Press:  09 April 2009

S. J. Bilchev ,
M. K. Grammatikopoulos  and
I. P. Stavroulakis
S. J. Bilchev
Affiliation:
Technical University7017 Rousse, Bulgaria
M. K. Grammatikopoulos
Affiliation:
University of Ioannina451 10 Ioannina, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the nth-order neutral differential equation 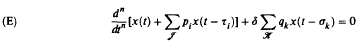where n ≥ 1, δ = ±1, I, K are initial segments of natural numbers, pi, τi, σk ∈ R and qk ≥ 0 for i ∈ I and k ∈ K. Then a necessary and sufficient condition for the oscillation of all solutions of (E) is that its characteristic equation 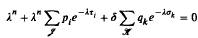has no real roots. The method of proof has the advantage that it results in easily verifiable sufficient conditions (in terms of the coefficients and the arguments only) for the oscillation of all solutionso of Equation (E).

MSC classification

Secondary: 34K40: Neutral equations 34C10: Oscillation theory, zeros, disconjugacy and comparison theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 52 , Issue 2 , April 1992 , pp. 261 - 284
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Arino, O. and Györi, I., ‘Necessary and sufficient conditions for oscillation of neutral differential system with several delays,’ J. Differential Equations 81 (1989), 98–105.CrossRefGoogle Scholar
[2]Bellman, R. and Cooke, K. L., Differential-difference equation (Academic Press, New York, 1963).CrossRefGoogle Scholar
[3]Brayton, R. K. and Willoughby, R. A., ‘On the numerical integration of a symmetric system of difference-differential equations of neutral type,’ J. Math. Anal. Appl. 18 (1967), 182–189.CrossRefGoogle Scholar
[4]Brumley, W. E., ‘On the asymptotic behavior of solutions of differential-difference equations of neutral type,’ J. Differential Equations 7 (1970), 175–188.CrossRefGoogle Scholar
[5]Driver, R. D., ‘Existence and continuous dependence of solutions of a neutral functional-differential equation,’ Arch. Ration. Mech. Anal. 19 (1965), 149–166.CrossRefGoogle Scholar
[6]Driver, R. D., ‘A mixed neutral system,’ Nonlinear Anal. 8 (1984), 155–158.CrossRefGoogle Scholar
[7]Farrell, K., ‘Necessary and sufficient conditions for oscillation of neutral equations with real coefficients,’ J. Math. Anal. Appl. 140 (1989), 251–261.CrossRefGoogle Scholar
[8]Fukagai, N. and Kusano, T., ‘Oscillation theory of first order functional differential equations with deviating arguments,’ Ann. Mat. Pura Appl. (14) 136 (1984), 95–117.CrossRefGoogle Scholar
[9]Grammatikopoulos, M. K., Grove, E. A. and Ladas, G., ‘Oscillation and asymptotic behavior of neutral differential equations with deviating arguments,’ Applicable Anal. 22 (1986), 1–19.CrossRefGoogle Scholar
[10]Grammatikopoulos, M. K., Sficas, Y. G. and Stavroulakis, I. P., ‘Necessary and sufficient conditions for oscillations of neutral equations with several coefficients,’ J. Differential Equations 76 (1988), 294–311.CrossRefGoogle Scholar
[11]Grammatikopoulos, M. K. and Stavroulakis, I. P., ‘Necessary and sufficient conditions for oscillation of neutral equations with deviating arguments,’ J. London Math. Soc. (2) 41 (1990), 244–260.CrossRefGoogle Scholar
[12]Grammatikopoulos, M. K. and Stavroulakis, I. P., ‘Oscillations of neutral differential equations’, Radovi Matematičiki 7 (1991), 47–71.Google Scholar
[13]Grove, E. A., Ladas, G. and Meimaridou, A., ‘A necessary and sufficient condition for the oscillation of neutral equations’, J. Math. Annal Appl. 126 (1987), 341–354.CrossRefGoogle Scholar
[14]Hale, J. K., ‘Stability of linear systems with delays’, Stability problems C.I.M.E., 06 1974, edited by Cremoneze, , pp. 19–35 (Roma 1974).Google Scholar
[15]Hale, J., Theory of functional differential equations (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
[16]Kulenović, M. R. S., Ladas, G. and Meimaridou, A., ‘Necessary and sufficient condition for oscillations of neutral differential equations’, J. Austral. Math. Soc. Ser. B 28 (1987), 362–375.CrossRefGoogle Scholar
[17]Ladas, G., Partheniadis, E. C. and Sficas, Y. G., ‘Necessary and sufficient conditions for oscillations of second-order neutral equations’, J. Math. Anal. Appl. 138 (1989), 214–231.CrossRefGoogle Scholar
[18]Ladas, G., Sficas, Y. O. and Stavroulakis, I. P., ‘Necessary and sufficient conditions for oscillations of higher order delay differential equations’, Trans. Amer. Math. Soc. 285 (1984), 81–90.CrossRefGoogle Scholar
[19]Ladas, G. and Stavroulakis, I. P., ‘On delay differential inequalities of higher order’, Canad. Math. Bull. 25 (1982), 348–354.CrossRefGoogle Scholar
[20]Ladas, G. and Stavroulakis, I. P., ‘Oscillations of differential equations of mixed type’, J. Math. Phys. Sci. 18 (1984), 245–262.Google Scholar
[21]Schultz, S. W., ‘Necessary and sufficient conditions for the oscillations of bounded solutions’, Applicable Anal. 30 (1988), 47–63.CrossRefGoogle Scholar
[22]Sficas, Y. G. and Stavroulakis, I. P., ‘Necessary and sufficient conditions for oscillations of neutral differential equations’, J. Math. Anal. Appl. 123 (1987), 494–507.CrossRefGoogle Scholar
[23]Slemrod, M. and Infante, E. F., ‘Asymptotic stability criteria for linear systems of difference-differential equations of neutral type and their discrete analogues’, J. Math. Anal. Appl. 38 (1972), 399–415.CrossRefGoogle Scholar
[24]Snow, W., ‘Existence, uniqueness, and stability for nonlinear differential-difference equation in the neutral case’, (N.Y.U. Courant Inst. Math. Sci. Rep. 1MM-NYU 328, February 1965).Google Scholar
[25]Wang, Z. C., ‘A necessary and sufficient condition for the oscillation of higher-order neutral equations’, Tōhuku Math. J. 41 (1989), 575–588.Google Scholar