Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T21:23:20.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation of a functional differential equation arising from an industrial problem

Part of: Qualitative theory

Published online by Cambridge University Press:  09 April 2009

Hiroshi Onose
Hiroshi Onose
Affiliation:
Department of Mathematics Ibaraki University Mito, 310 Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the last few years, the oscillatory behavior of functional differential equations has been investigated by many authors. But much less is known about the first-order functional differential equations. Recently, Tomaras (1975b) considered the functional differential equation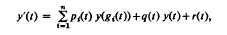 and gave very interesting results on this problem, namely the sufficient conditions for its solutions to oscillate. The purpose of this paper is to extend and improve them, by examining the more general functional differential equation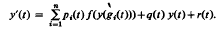

MSC classification

Secondary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 26 , Issue 3 , November 1978 , pp. 323 - 329
Copyright
Copyright © Australian Mathematical Society 1978

References

Kato, Tosio (1972), ‘Asymptotic behaviour of solutions of the functional differential equation y′(x) = ay(λx) + by(x)’, Delay and functional differential equations and their applications, pp. 197–217 (Proc. Conf. Park City, Utah, 1972. Academic Press, New York, London, 1972).CrossRefGoogle Scholar
Kato, Tosio and McLeod, J. B. (1971), ‘The functional-differential equation y′(x) = ay(λx)+by(x)’, Bull. Amer. Math. Soc. 77, 891–937.Google Scholar
Kusano, T. and Onose, H. (1974), ‘Oscillations of functional differential equations with retarded argument’, J. Differential Equations, 15, 269–277.CrossRefGoogle Scholar
Ladas, G., Lakshmikantham, V. and Papadakis, J. S. (1972), ‘Oscillations of higher-order retarded differential equations generated by the retarded argument’, Delay and functional differential equations and their applications pp. 219–231, (Proc. Conf. Park City, Utah, 1972. Academic Press, New York, London, 1972).CrossRefGoogle Scholar
Tomaras, Alexander (1975a), ‘Oscillations of an equation relevant to an industrial problem’, Bull. Austral. Math. Soc. 12, 425–431.CrossRefGoogle Scholar
Tomaras, Alexander (1975b), ‘Oscillatory behaviour of an equation arising from an industrial problem’, Bull. Austral. Math. Soc. 13, 255–260.CrossRefGoogle Scholar