No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
If M is a commutative W*-algebra of operators and if ReM is the Dedekind complete Riesz space of self-adjoint elements of M, then it is shown that the set 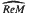 of densely defined self-adjoint transformations affiliated with ReM is a Dedekind complete, laterally complete Riesz algebra containing ReM as an order dense ideal. The Riesz algebra of densely defined orthomorphisms on ReM is shown to coincide with
of densely defined self-adjoint transformations affiliated with ReM is a Dedekind complete, laterally complete Riesz algebra containing ReM as an order dense ideal. The Riesz algebra of densely defined orthomorphisms on ReM is shown to coincide with 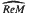 , and via the vector lattice Randon-Nikodym theorem of Luxemburg and Schep, it is shown that the lateral completion of ReM may be identified with the extended order dual of ReM.
, and via the vector lattice Randon-Nikodym theorem of Luxemburg and Schep, it is shown that the lateral completion of ReM may be identified with the extended order dual of ReM.