No CrossRef data available.
Published online by Cambridge University Press: 15 November 2021
We show that, given a compact minimal system
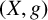 $(X,g)$
and an element h of the topological full group
$(X,g)$
and an element h of the topological full group
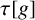 $\tau [g]$
of g, the infinite orbits of h admit a locally constant orientation with respect to the orbits of g. We use this to obtain a clopen partition of
$\tau [g]$
of g, the infinite orbits of h admit a locally constant orientation with respect to the orbits of g. We use this to obtain a clopen partition of
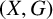 $(X,G)$
into minimal and periodic parts, where G is any virtually polycyclic subgroup of
$(X,G)$
into minimal and periodic parts, where G is any virtually polycyclic subgroup of
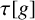 $\tau [g]$
. We also use the orientation of orbits to give a refinement of the index map and to describe the role in
$\tau [g]$
. We also use the orientation of orbits to give a refinement of the index map and to describe the role in
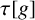 $\tau [g]$
of the submonoid generated by the induced transformations of g. Finally, we consider the problem, given a homeomorphism h of the Cantor space X, of determining whether or not there exists a minimal homeomorphism g of X such that
$\tau [g]$
of the submonoid generated by the induced transformations of g. Finally, we consider the problem, given a homeomorphism h of the Cantor space X, of determining whether or not there exists a minimal homeomorphism g of X such that
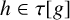 $h \in \tau [g]$
.
$h \in \tau [g]$
.
Communicated by Anthony Henderson
Research funded by ARC project FL170100032.