The order cycle system of stock control can be formulated as follows: demands for stock occur according to some pattern which we call the demand process and specify in detail later in this section. At fixed intervals of time orders are placed to replenish stock. Let orders for stock be placed at the instants jN, j = 1,2, …; the interval [(j — 1)(N, jN) which we suppose closed at its lower end-point and open at its upper end-point, is called the j-th order cycle and N the length of this interval is called the order cycle period. We suppose that an order placed at time jN is delivered into stock at time jN + li where {li} is a sequence of non-negative random variables independent of the demand process and the order cycle period, we suppose also that the li are mutually independent and identically distributed with common distribution function L(x) with L(0 +) = 0 and finite expectation 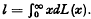. The quantity li is called the lead time of the j-th order, that is of the order placed at jN and is supposed independent of the amount ordered. That portion of a demand, if any, which cannot be satisfied immediately is satisfied from future deliveries, thus every demand is satisfied eventually and a negative inventory or back orders can be held. We shall suppose that all order cycle periods under consideration are multiples of some fixed time interval of length τ which we shall take as our unit of time. For example, the interval of length τ could be one day and we would consider order cycle periods which were integral multiples of days. For convenience we take τ = 1 and suppose that the order cycle peiod N is an integer. In this paper we shall consider the following two demand processes.