Published online by Cambridge University Press: 14 March 2016
The optimistic limit is a mathematical formulation of the classical limit, which is a physical method to estimate the actual limit by using the saddle-point method of a certain potential function. The original optimistic limit of the Kashaev invariant was formulated by Yokota, and a modified formulation was suggested by the author and others. This modified version is easier to handle and more combinatorial than the original one. On the other hand, it is known that the Kashaev invariant coincides with the evaluation of the colored Jones polynomial at a certain root of unity. This optimistic limit of the colored Jones polynomial was also formulated by the author and others, but it is very complicated and needs many unnatural assumptions. In this article, we suggest a modified optimistic limit of the colored Jones polynomial, following the idea of the modified optimistic limit of the Kashaev invariant, and show that it determines the complex volume of a hyperbolic link. Furthermore, we show that this optimistic limit coincides with the optimistic limit of the Kashaev invariant modulo 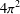 $4{\it\pi}^{2}$. This new version is easier to handle and more combinatorial than the old version, and has many advantages over the modified optimistic limit of the Kashaev invariant. Because of these advantages, several applications have already appeared and more are in preparation.
$4{\it\pi}^{2}$. This new version is easier to handle and more combinatorial than the old version, and has many advantages over the modified optimistic limit of the Kashaev invariant. Because of these advantages, several applications have already appeared and more are in preparation.