Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T17:02:18.515Z Has data issue: false hasContentIssue false
  • English
  • Français

OPERATOR SYSTEM NUCLEARITY VIA $C^{\ast }$ -ENVELOPES

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators Methods of category theory in functional analysis Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  11 May 2016

VED PRAKASH GUPTA  and
PREETI LUTHRA
VED PRAKASH GUPTA*
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi 110067, India email [email protected]
PREETI LUTHRA
Affiliation:
Department of Mathematics, University of Delhi, Delhi 110007, India email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that an operator system is (min, ess)-nuclear if its 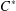$C^{\ast }$ -envelope is nuclear. This allows us to deduce that an operator system associated to a generating set of a countable discrete group by Farenick et al. [‘Operator systems from discrete groups’, Comm. Math. Phys.329(1) (2014), 207–238] is (min, ess)-nuclear if and only if the group is amenable. We also make a detailed comparison between ess and other operator system tensor products and show that an operator system associated to a minimal generating set of a finitely generated discrete group (respectively, a finite graph) is (min, max)-nuclear if and only if the group is of order less than or equal to three (respectively, every component of the graph is complete).

Keywords

operator systemsamenable groupsgraphsnuclearityC ∗ -envelopestensor products

MSC classification

Primary: 46L06: Tensor products of $C^*$-algebras 46L07: Operator spaces and completely bounded maps
Secondary: 47L25: Operator spaces (= matricially normed spaces) 46M05: Tensor products 46B28: Spaces of operators; tensor products; approximation properties
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 3 , December 2016 , pp. 356 - 375
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Argerami, M. and Farenick, D., ‘The C*-envelope of an irreducible periodic weighted unilateral shift’, Integral Equations Operator Theory 77(2) (2013), 199–210.CrossRefGoogle Scholar
Argerami, M. and Farenick, D., ‘C*-envelopes of Jordan operator systems’, Oper. Matrices 9(2) (2015), 325–341.CrossRefGoogle Scholar
Arveson, W., ‘Subalgebras of C*-algebras’, Acta Math. 123 (1969), 141–224.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., C*-Algebras and Finite-Dimensional Approximations, Vol. 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Choi, M.-D. and Effros, E. G., ‘Injectivity and operator spaces’, J. Funct. Anal. 24(2) (1977), 156–209.CrossRefGoogle Scholar
Effros, E. G. and Ruan, Z.-J., Operator Spaces, London Mathematical Society Monographs (Oxford University Press, New York, 2000).Google Scholar
Farenick, D., Kavruk, A. S. and Paulsen, V. I., ‘C*-algebras with the weak expectation property and a multivariable analogue of Ando’s theorem on the numerical radius’, J. Operator Theory 70(2) (2013), 573–590.CrossRefGoogle Scholar
Farenick, D., Kavruk, A. S., Paulsen, V. I. and Todorov, I. G., ‘Operator systems from discrete groups’, Comm. Math. Phys. 329(1) (2014), 207–238.CrossRefGoogle Scholar
Farenick, D. and Paulsen, V. I., ‘Operator system quotients of matrix algebras and their tensor products’, Math. Scand. 111(2) (2012), 210–243.CrossRefGoogle Scholar
Gupta, V. P., Mandayam, P. and Sunder, V. S., The Functional Analysis of Quantum Information Theory, Lecture Notes in Physics, 902 (Springer, Cham, 2015).CrossRefGoogle Scholar
Hamana, M., ‘Injective envelopes of operator systems’, Publ. Res. Inst. Math. Sci. 15(3) (1979), 773–785.CrossRefGoogle Scholar
Han, K. H., ‘On maximal tensor products and quotient maps of operator systems’, J. Math. Anal. Appl. 384(2) (2011), 375–386.CrossRefGoogle Scholar
Han, K. H. and Paulsen, V. I., ‘An approximation theorem for nuclear operator systems’, J. Funct. Anal. 261(4) (2011), 999–1009.CrossRefGoogle Scholar
Kavruk, A. S., ‘Nuclearity related properties in operator systems’, J. Operator Theory 71(1) (2014), 95–156.CrossRefGoogle Scholar
Kavruk, A. S., Paulsen, V. I., Todorov, I. G. and Tomforde, M., ‘Tensor products of operator systems’, J. Funct. Anal. 261(2) (2011), 267–299.CrossRefGoogle Scholar
Kavruk, A. S., Paulsen, V. I., Todorov, I. G. and Tomforde, M., ‘Quotients, exactness, and nuclearity in the operator system category’, Adv. Math. 235 (2013), 321–360.CrossRefGoogle Scholar
Kirchberg, E. and Wassermann, S., ‘C*-algebras generated by operator systems’, J. Funct. Anal. 155(2) (1998), 324–351.CrossRefGoogle Scholar
Lance, C., ‘On nuclear C*-algebras’, J. Funct. Anal. 12 (1973), 157–176.CrossRefGoogle Scholar
Ortiz, C. M. and Paulsen, V. I., ‘Lovász theta type norms and operator systems’, Linear Algebra Appl. 477 (2015), 128–147.CrossRefGoogle Scholar
Paulsen, V. I., Completely Bounded Maps and Operator Algebras, Vol. 78 (Cambridge University Press, Cambridge, 2002).Google Scholar
Pisier, G., Introduction to Operator Space Theory, London Mathematical Society Lecture Note Series, 294 (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar