Published online by Cambridge University Press: 09 April 2009
If C is a class of groups, we denote by RC the class of groups which are residually in C i.e. G ∈ RC if and only if 1 ≠ g ∈ G implies that there exists a normal subgroup N of G such that g ∈ N and G/N ∈ C. A group G is residually a finite p-group if it belongs RFp, where Fp denotes the class of finite p-groups. One also says that the groups in RFp are residually of order equal to a power of the prime p. Given a group G with one defining relator r, one might ask for conditions on the “form” of the relator that would guarantee that G have certain residual properties. In this context, Baumslag (1971) has proved that if all the exponents of the generators appearing in r are positive, then G is residually solvable. In the same paper he also concerned himself with the residual nilpotence of one-relator groups, and found that the situation there was much more complicated. If one goes one step further and asks for conditions that will ensure that for a given prime p the one-relator group be residually a finite p-group, then very little seems to be known. Of course, if one takes r to be one of the generators: 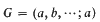 then G is freely generated by the remaining generators, and hence is in RFp for all primes p (Mahec (1949), Lazard (1965), 3.1.4). Our main purpose in this paper is to develop methods of generating examples of one-relator groups that are residually of order equal to a given prime p.
then G is freely generated by the remaining generators, and hence is in RFp for all primes p (Mahec (1949), Lazard (1965), 3.1.4). Our main purpose in this paper is to develop methods of generating examples of one-relator groups that are residually of order equal to a given prime p.