Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T14:18:28.726Z Has data issue: false hasContentIssue false
  • English
  • Français

ONE-POINT CONNECTIFICATIONS

Part of: Fairly general properties Basic constructions

Published online by Cambridge University Press:  09 January 2015

M. R. KOUSHESH
M. R. KOUSHESH*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A space 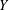$Y$ is called an extension of a space 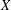$X$ if 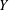$Y$ contains 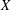$X$ as a dense subspace. An extension 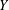$Y$ of 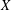$X$ is called a one-point extension if 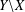$Y\setminus X$ is a singleton. Compact extensions are called compactifications and connected extensions are called connectifications. It is well known that every locally compact noncompact space has a one-point compactification (known as the Alexandroff compactification) obtained by adding a point at infinity. A locally connected disconnected space, however, may fail to have a one-point connectification. It is indeed a long-standing question of Alexandroff to characterize spaces which have a one-point connectification. Here we prove that in the class of completely regular spaces, a locally connected space has a one-point connectification if and only if it contains no compact component.

Keywords

Stone–Čech compactificationWallman compactificationone-point extensionone-point connectificationone-point compactificationlocally connected

MSC classification

Primary: 54D35: Extensions of spaces (compactifications, supercompactifications, completions, etc.)
Secondary: 54D05: Connected and locally connected spaces (general aspects) 54D40: Remainders 54B15: Quotient spaces, decompositions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 1 , August 2015 , pp. 76 - 84
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abry, M., Dijkstra, J. J. and van Mill, J., ‘On one-point connectifications’, Topology Appl. 154(3) (2007), 725–733.CrossRefGoogle Scholar
Alas, O., Tkačenko, M., Tkachuk, V. and Wilson, R., ‘Connectifying some spaces’, Topology Appl. 71(3) (1996), 203–215.CrossRefGoogle Scholar
Alexandroff, P., ‘Über die Metrisation der im Kleinen kompakten topologischen Räume’, Math. Ann. 92(3–4) (1924), 294–301 (in German).CrossRefGoogle Scholar
Burke, D. K., ‘Covering properties’, in: Handbook of Set-Theoretic Topology (North-Holland, Amsterdam, 1984), 347–422.Google Scholar
Engelking, R., General Topology, 2nd edn (Heldermann, Berlin, 1989).Google Scholar
Gillman, L. and Jerison, M., Rings of Continuous Functions (Springer, New York–Heidelberg, 1976).Google Scholar
Gruenhage, G., Kulesza, J. and Le Donne, A., ‘Connectifications of metrizable spaces’, Topology Appl. 82(1–3) (1998), 171–179.CrossRefGoogle Scholar
Knaster, B., ‘Sur un problème de P. Alexandroff’, Fund. Math. 33 (1945), 308–313.CrossRefGoogle Scholar
Koushesh, M. R., ‘On order structure of the set of one-point Tychonoff extensions of locally compact spaces’, Topology Appl. 154(14) (2007), 2607–2634.CrossRefGoogle Scholar
Koushesh, M. R., ‘Compactification-like extensions’, Dissertationes Math. (Rozprawy Mat.) 476 (2011), 88 pages.Google Scholar
Koushesh, M. R., ‘The partially ordered set of one-point extensions’, Topology Appl. 158(3) (2011), 509–532.CrossRefGoogle Scholar
Koushesh, M. R., ‘A pseudocompactification’, Topology Appl. 158(16) (2011), 2191–2197.CrossRefGoogle Scholar
Koushesh, M. R., ‘One-point extensions of locally compact paracompact spaces’, Bull. Iranian Math. Soc. 37(4) (2011), 199–228.Google Scholar
Koushesh, M. R., ‘One-point extensions and local topological properties’, Bull. Aust. Math. Soc. 88(1) (2013), 12–16.CrossRefGoogle Scholar
Koushesh, M. R., ‘Topological extensions with compact remainder’, J. Math. Soc. Japan 67(1) (2015), 1–42.CrossRefGoogle Scholar
Mrówka, S., ‘On local topological properties’, Bull. Acad. Polon. Sci. Cl. III 5 (1957), 951–956.Google Scholar
Porter, J. R. and Woods, R. G., Extensions and Absolutes of Hausdorff Spaces (Springer, New York, 1988).CrossRefGoogle Scholar
Porter, J. R. and Woods, R. G., ‘Subspaces of connected spaces’, Topology Appl. 68(2) (1996), 113–131.CrossRefGoogle Scholar
Stephenson, R. M. Jr., ‘Initially 𝜅-compact and related spaces’, in: Handbook of Set-Theoretic Topology (North-Holland, Amsterdam, 1984), 603–632.Google Scholar
Vaughan, J. E., ‘Countably compact and sequentially compact spaces’, in: Handbook of Set-Theoretic Topology (North-Holland, Amsterdam, 1984), 569–602.Google Scholar
Watson, S. and Wilson, R., ‘Embeddings in connected spaces’, Houston J. Math. 19(3) (1993), 469–481.Google Scholar