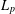Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T17:52:01.048Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE VARIATIONAL CONSTANT ASSOCIATED TO THE $L_{p}$-HARDY INEQUALITY

Part of: Inequalities General theory of linear operators Linear function spaces and their duals

Published online by Cambridge University Press:  23 September 2016

A. D. WARD
A. D. WARD*
Affiliation:
NZ Institute of Advanced Study, Massey University, Private Bag 102 904, North Shore MSC, 0745 Auckland, New Zealand email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 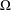$\unicode[STIX]{x1D6FA}$ be a domain in 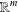$\mathbb{R}^{m}$ with nonempty boundary. In Ward [‘On essential self-adjointness, confining potentials and the 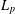$L_{p}$-Hardy inequality’, PhD Thesis, NZIAS Massey University, New Zealand, 2014] and [‘The essential self-adjointness of Schrödinger operators on domains with non-empty boundary’, Manuscripta Math.150(3) (2016), 357–370] it was shown that the Schrödinger operator 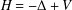$H=-\unicode[STIX]{x1D6E5}+V$, with domain of definition 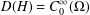$D(H)=C_{0}^{\infty }(\unicode[STIX]{x1D6FA})$ and 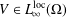$V\in L_{\infty }^{\text{loc}}(\unicode[STIX]{x1D6FA})$, is essentially self-adjoint provided that 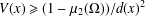$V(x)\geq (1-\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA}))/d(x)^{2}$. Here 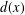$d(x)$ is the Euclidean distance to the boundary and 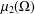$\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is the nonnegative constant associated to the 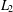$L_{2}$-Hardy inequality. The conditions required for a domain to admit an 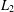$L_{2}$-Hardy inequality are well known and depend intimately on the Hausdorff or Aikawa/Assouad dimension of the boundary. However, there are only a handful of domains where the value of 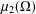$\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is known explicitly. By obtaining upper and lower bounds on the number of cubes appearing in the 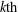$k\text{th}$ generation of the Whitney decomposition of 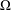$\unicode[STIX]{x1D6FA}$, we derive an upper bound on 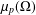$\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x1D6FA})$, for 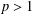$p>1$, in terms of the inner Minkowski dimension of the boundary.

Keywords

Lp -Hardy inequalityvariational constantsessential self-adjointness

MSC classification

Primary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Secondary: 47A63: Operator inequalities 47A05: General (adjoints, conjugates, products, inverses, domains, ranges, etc.) 26D15: Inequalities for sums, series and integrals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 3 , June 2017 , pp. 405 - 419
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Barbatis, G., Filippas, S. and Tertikas, A., ‘A unified approach to improved L p Hardy inequalities with best constants’, Trans. Amer. Math. Soc. 356(6) (2003), 2169–2196.Google Scholar
Barbatis, G., Filippas, S. and Tertikas, A., ‘Series expansions for L p Hardy inequalities’, Indiana Univ. Math. J. 52(1) (2003), 171–190.Google Scholar
Davies, E. B., A Review of Hardy Inequalities, The Maz’ya Anniversary Collection (Birkhäuser, Basel, 1999).Google Scholar
Eastham, M. S. P., Evans, W. D. and Mcleod, J. B., ‘The essential self-adjointness of Schrödinger type operators’, Arch. Ration. Mech. Anal. 60(2) (1976), 185–204.Google Scholar
Edmunds, D. E. and Evans, W. D., Hardy Operators, Function Spaces and Embeddings (Springer, Berlin, 2004).CrossRefGoogle Scholar
Evans, W. D. and Harris, D. J., ‘Fractals, trees and the Neumann laplacian’, Math. Ann. 296 (1993), 493–527.Google Scholar
Kinnunen, J. and Korte, R., ‘Characterizations for Hardys inequality’, in: Around the Research of Vladimir Mazya I (Springer, New York, 2010), 239–254.Google Scholar
Kinnunen, J. and Martio, O., ‘Hardy’s inequalities for Sobolev functions’, Math. Res. Lett. 4 (1997), 489–500.Google Scholar
Korte, R., Lehrbäck, J. and Tuominen, H., ‘The equivalence between pointwise Hardy inequalities and uniform fatness’, Math. Ann. 351(3) (2011), 711–731.Google Scholar
Koskela, P. and Zhong, X., ‘Hardy’s inequality and the boundary size’, Proc. Amer. Math. Soc. 131(4) (2002), 1151–1158.Google Scholar
Lapidus, M. L., Rock, J. A. and Zubrinić, D., ‘Box-counting fractal strings, zeta functions, and equivalent forms of Minkowski dimension’, arXiv:1207.6681, 2012.Google Scholar
Lehrbäck, J., ‘Weighted Hardy inequalities and the size of the boundary’, Manuscripta Math. 127 (2008), 249–273.CrossRefGoogle Scholar
Lehrbäck, J., ‘Pointwise Hardy inequalities and uniformly fat sets’, Proc. Amer. Math. Soc. 136(6) (2008), 2193–2200.Google Scholar
Lewis, J. L., ‘Uniformly fat sets’, Trans. Amer. Math. Soc. 308(1) (1988), 177–196.Google Scholar
Martio, O. and Vuorinen, M., ‘Whitney cubes, p-capacity and Minkowski content’, Exp. Math. 5 (1987), 17–40.Google Scholar
Reed, M. C. and Simon, B., Methods of Modern Mathematical Physics, Vol. 2 Fourier Analysis and Self-Adjointness (Academic Press, New York, 1975).Google Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions (Princeton University Press, Princeton, NJ, 1970).Google Scholar
Ward, A. D., ‘On essential self-adjointness, confining potentials and the $L_{p}$ -Hardy inequality’, PhD Thesis, NZIAS Massey University, New Zealand, 2014.Google Scholar
Ward, A. D., ‘The essential self-adjointness of Schrödinger operators on domains with non-empty boundary’, Manuscripta Math. 150(3) (2016), 357–370.Google Scholar
Zubrinić, D., ‘Minkowski content and singular integrals’, Chaos, Solitons and Fractals 17 (2003), 169–177.Google Scholar
Zubrinić, D., ‘Analysis of Minkowski contents of fractal sets and applications’, Real Anal. Exchange 31(2) (2005), 315–354.Google Scholar