Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rhoades, B. E.
1992.
The spectra of weighted mean operators on bν0.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 52,
Issue. 2,
p.
242.
Yildirim, Mustafa
2003.
ON THE SPECTRUM OF THE RHALY OPERATORS ON bv0.
Communications of the Korean Mathematical Society,
Vol. 18,
Issue. 4,
p.
669.
Bilgiç, Hüseyin
and
Furkan, Hasan
2007.
On the fine spectrum of the operator B(r,s,t) over the sequence spaces ℓ1 and bv.
Mathematical and Computer Modelling,
Vol. 45,
Issue. 7-8,
p.
883.
Bilgiç, Hüseyin
and
Furkan, Hasan
2008.
On the fine spectrum of the generalized difference operator over the sequence spaces and.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 68,
Issue. 3,
p.
499.
Furkan, Hasan
Bi̇lgi̇ç, Hüseyi̇n
and
Başar, Feyzi
2010.
On the fine spectrum of the operator B(r,s,t) over the sequence spaces ℓp and bvp,(1<p<∞).
Computers & Mathematics with Applications,
Vol. 60,
Issue. 7,
p.
2141.
Tripathy, Binod Chandra
and
Paul, Avinoy
2011.
Spectrum of the operator B(f, g) on the vector valued sequence space c_0(X).
Boletim da Sociedade Paranaense de Matemática,
Vol. 31,
Issue. 1,
p.
105.
Karaisa, Ali
and
Vecchio, Antonia
2012.
Fine Spectra of Upper Triangular Double‐Band Matrices over the Sequence Space ℓp, (1 < p < ∞).
Discrete Dynamics in Nature and Society,
Vol. 2012,
Issue. 1,
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2013.
Convergence of arithmetic means of operators in Fréchet spaces.
Journal of Mathematical Analysis and Applications,
Vol. 401,
Issue. 1,
p.
160.
Dutta, Amar Jyoti
and
Tripathy, Binod Chandra
2013.
Fine Spectrum of the Generalized Difference Operator B(r,s) over the Class of Convergent Series.
International Journal of Analysis,
Vol. 2013,
Issue. ,
p.
1.
Karaisa, Ali
and
Başar, Feyzi
2013.
Fine Spectra of Upper Triangular Triple-Band Matrices over the Sequence Space ().
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Tripathy, Binod Chandra
and
Paul, Avinoy
2013.
The Spectrum of the Opertator D(r, 0, 0, s) over the Sequence Spaces c0and c.
Kyungpook mathematical journal,
Vol. 53,
Issue. 2,
p.
247.
Tripathy, Binod Chandra
and
Paul, Avinoy
2015.
The spectrum of the operator $$ D( r,0, s,0,t)$$ D ( r , 0 , s , 0 , t ) over the sequence spaces $$\ell _{p}$$ ℓ p and $$bv_{p}$$ b v p.
Afrika Matematika,
Vol. 26,
Issue. 5-6,
p.
1137.
ALBANESE, ANGELA A.
BONET, JOSÉ
and
RICKER, WERNER J.
2015.
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED SPACES.
Journal of the Australian Mathematical Society,
Vol. 99,
Issue. 3,
p.
287.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2016.
Mean ergodicity and spectrum of the Cesàro operator on weighted $$c_0$$ c 0 spaces.
Positivity,
Vol. 20,
Issue. 4,
p.
761.
Das, Rituparna
2017.
Spectrum and fine spectrum of the Zweier matrix over the sequence space cs.
Boletim da Sociedade Paranaense de Matemática,
Vol. 35,
Issue. 2,
p.
209.
Mursaleen, Mohammad
Yildirim, Mustafa
and
Durna, Nuh
2018.
On the spectrum and Hilbert Schimidt properties of generalized Rhaly matrices.
Communications Faculty Of Science University of Ankara Series A1Mathematics and Statistics,
Vol. 68,
Issue. 1,
p.
712.
El-Shabrawy, Saad R.
and
Abu-Janah, Suad H.
2018.
Spectra of the generalized difference operator on the sequence spaces andh.
Linear and Multilinear Algebra,
Vol. 66,
Issue. 8,
p.
1691.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2018.
The Cesàro operator in weighted ℓ1 spaces.
Mathematische Nachrichten,
Vol. 291,
Issue. 7,
p.
1015.
Yeşilkayagil, Medine
and
Başar, Feyzi
2019.
A Survey for the Spectrum of Triangles over Sequence Spaces.
Numerical Functional Analysis and Optimization,
Vol. 40,
Issue. 16,
p.
1898.
Sawano, Yoshihiro
and
El-Shabrawy, Saad R.
2020.
Fine spectra of the discrete generalized Cesàro operator on Banach sequence spaces.
Monatshefte für Mathematik,
Vol. 192,
Issue. 1,
p.
185.


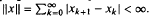 .
.