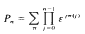Schur's matrix Mn is ordinarily defined to be the n by n matrix (εjk), 0 ≦ j, k < n, where ε = exp (2 πi/n). This matrix occurs in a variety of areas including number theory, statistics, coding theory and combinatorics. In this paper, we investigate Pn, the permanent of Mn, which is define by where π ranges over all n! permutations on {0,1, …, n – 1}. Pn occurs, for example, in the study of circulants. Specifically, let Xn denote the n by n circulant matrix (xi, j) with xi, j = xi, j, where the subscript is reduced modulo n. The determinant of Xn is a homogeneous polynomial of degree n in the xi and can be written as 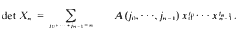Then Pn = A (1,1, … 1). Typical of the results established in this note are: (i) P2n = 0 for all n, (ii) Pp ≡ p ! (mod p3) for p a prime >3. (iii) If pa divides n then 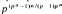divides Pn. Also, a table of values of Pn is given for 1 ≦ n ≦ 23.