Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T23:00:56.909Z Has data issue: false hasContentIssue false
  • English
  • Français

On the orders of conjugacy classes in group algebras of p-groups

Part of: Conditions on elements Representation theory of groups Rings and algebras arising under various constructions

Published online by Cambridge University Press:  09 April 2009

A. Bovdi ,
L. G. Kovács  and
S. Mihovski
A. Bovdi
Affiliation:
University of Debrecen, 4010 Debrecen, Hungary e-mail: [email protected]
L. G. Kovács
Affiliation:
Australian National University, Canberra ACT 0200, Australia e-mail: [email protected]
S. Mihovski
Affiliation:
University of Plovdiv, 4000 Plovdiv, Bulgaria e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be a prime, 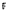a field of pn elements, and G a finite p-group. It is shown here that if G has a quotient whose commutator subgroup is of order p and whose centre has index pk, then the group of normalized units in the group algebra 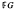has a conjugacy class of pnk elements. This was first proved by A. Bovdi and C. Polcino Milies for the case k = 2; their argument is now generalized and simplified. It remains an intriguing question whether the cardinality of the smallest noncentral conjugacy class can always be recognized from this test.

Keywords

group algebragroup of unitsconjrgacy classfinite p-group

MSC classification

Secondary: 16S34: Group rings , Laurent polynomial rings 16U60: Units, groups of units 20C05: Group rings of finite groups and their modules
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 77 , Issue 2 , October 2004 , pp. 185 - 190
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Bovdi, A., ‘The group of units of group algebras of characteristic p’, Publ. Math. Debrecen 52 (1998), 193–244.CrossRefGoogle Scholar
[2]Bovdi, A. and Milies, C. Polcino, ‘Conjugacy classes of the group of units in group algebras of finite p-groups’, An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 8 (2000), 1–12.Google Scholar
[3]Bovdi, A. and Milies, C. Polcino, ‘Normal subgroups of the group of units in group rings of torsion groups’, Publ. Math. Debrecen 59 (2001), 235–242.CrossRefGoogle Scholar
[4]Bovdi, V. and Dokuchaev, M., ‘Group algebras whose involutory units commute’, Algebra Colloq. 9 (2002), 49–64.Google Scholar