There are infinitely, but at most continuously, many varieties of groups; the precise cardinal is unknown. It is easy to see that if there is no infinite properly descending chain of varieties (equivalently, if the laws of every variety have a finite basis), then the number of varieties is countable infinity; the converse implication does not seem to have been proved. This note presents an argument which implies that if the locally finite or the locally nilpotent varieties fail to satisfy the minimum condition, then there are continuously many such varieties. Alternatively, one can conclude that if a locally finite or locally nilpotent variety 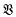has a finite basis for its laws but some subvariety 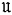of 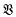has none, then there are continuously many varieties between 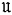and 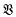. This points again to the interesting question: is every locally finite [locally nilpotent] variety 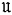contained in a suitable locally finite [locally nilpotent] variety 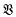which has a finite basis for its laws? (That is, must be locally finite [locally nilpotent] for some finite n?) For, if the answer were affirmative, it would follow that the number of locally finite [locally nilpotent] varieties is either countable or the cardinal of the continuum, depending exactly on the existence of finite bases for the laws of such varieties.