Article contents
ON THE NUMBER OF SUBSEMIGROUPS OF DIRECT PRODUCTS INVOLVING THE FREE MONOGENIC SEMIGROUP
Published online by Cambridge University Press: 01 February 2019
Abstract
The direct product 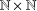 $\mathbb{N}\times \mathbb{N}$ of two free monogenic semigroups contains uncountably many pairwise nonisomorphic subdirect products. Furthermore, the following hold for
$\mathbb{N}\times \mathbb{N}$ of two free monogenic semigroups contains uncountably many pairwise nonisomorphic subdirect products. Furthermore, the following hold for 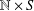 $\mathbb{N}\times S$, where
$\mathbb{N}\times S$, where 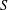 $S$ is a finite semigroup. It contains only countably many pairwise nonisomorphic subsemigroups if and only if
$S$ is a finite semigroup. It contains only countably many pairwise nonisomorphic subsemigroups if and only if 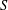 $S$ is a union of groups. And it contains only countably many pairwise nonisomorphic subdirect products if and only if every element of
$S$ is a union of groups. And it contains only countably many pairwise nonisomorphic subdirect products if and only if every element of 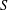 $S$ has a relative left or right identity element.
$S$ has a relative left or right identity element.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by



