Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T01:27:44.614Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of real roots of a random algebraic equation

Part of: Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  09 April 2009

D. Pratihari ,
R. K. Panda  and
B. P. Pattanaik
D. Pratihari
Affiliation:
College of Basic Sciences & HumanitiesBhubaneswar - 751 003, Orissa, INDIA
R. K. Panda
Affiliation:
College of Basic Sciences & HumanitiesBhubaneswar - 751 003, Orissa, INDIA
B. P. Pattanaik
Affiliation:
College of Basic Sciences & HumanitiesBhubaneswar - 751 003, Orissa, INDIA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Nn(ω) be the number of real roots of the random algebraic equation Σnv = 0 avξv (ω)xv = 0, where the ξv(ω)'s are independent, identically distributed random variables belonging to the domain of attraction of the normal law with mean zero and P{ξv(ω) ≠ 0} > 0; also the av 's are nonzero real numbers such that (kn/tn) = 0(log n) where kn = max0≤v≤n |av| and tn = min0≤v≤n |av|. It is shown that for any sequence of positive constants (εn, n ≥ 0) satisfying εn → 0 and ε2nlog n → ∞ there is a positive constant μ so that 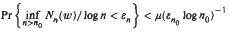for all n0 sufficiently large.

Keywords

Independentidentically distributed random variablesrandom algebraic equationreal rootsdomain of attraction of the normal lawslowly varying function.

MSC classification

Secondary: 60B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 54 , Issue 1 , February 1993 , pp. 86 - 96
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Hajek, J. and Renyi, A., ‘A generalisation of an inequality of Kolmogorov’, Acta Math. Hungar. 6 (1955), 281–283.Google Scholar
[2]Ibragimov, I. A. and Maslova, N. B., ‘On the expected number of real zeros of random algebraic polynomials I. Coefficients with zero means’ (translated by Seckler, B.), Theory Probab. Appl. 16 (1971), 228–248.CrossRefGoogle Scholar
[3]Ibragimov, I. A. and Linnik, Yu. V., Independent and stationary sequences of random variables (Wolters-Noordhoff, Groningen, 1972).Google Scholar
[4]Mishra, M. N., Nayak, N. N. and Pattanayak, S., ‘Lower bound of the number of real roots of a random algebraic polynomial’, J. Indian Math. Soc. 45 (1981), 285–296.Google Scholar
[5]Mishra, M. N., Nayak, N. N. and Pattanayak, S., ‘Strong result for real zeros of random polynomials’, Pac. J. Math. 103 (1982), 509–522.CrossRefGoogle Scholar
[6]Mishra, M. N., Nayak, N. N. and Pattanayak, S., ‘Lower bound for the number of real roots of a random algebraic polynomial’, J. Austral. Math. Soc. Series A 35 (1983), 18–27.Google Scholar
[7]Samal, G., ‘On the number of real roots of a random algebraic equation’, Proc. Camb. Philos. Soc. 58 (1962) 433–442.CrossRefGoogle Scholar
[8]Samal, G., and Pratihari, D., ‘Strong result for real zeros of random polynomials’, J. Indian Math. Soc. 40 (1976), 223–234.Google Scholar
[9]Samal, G., and Pratihari, D., ‘Strong result for real zeros of random polynomials II’, J. Indian Math. Soc. 41 (1977), 395–403.Google Scholar
[10]Samal, G., and Pratihari, D., ‘Number of real zeros of a random algebraic polynomial’, Indian J. Math. 20 (3) (1978), 225–232.Google Scholar