Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T02:09:08.913Z Has data issue: false hasContentIssue false
  • English
  • Français

On The Maximum of the Geometric Moving Average

Published online by Cambridge University Press:  09 April 2009

A. M. Hasofer
A. M. Hasofer
Affiliation:
Australian National UniversityCanberra, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By the geometric moving average of the independent, identically distributed random variables {Xn}, we mean the stochastic process 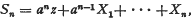, where a is a real number such that 0≦a≦1.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 9 , Issue 1-2 , February 1969 , pp. 100 - 108
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Feller, W., An introduction to probability theory and its applications (Vol. II., Wiley & Sons, New York, 1966).Google Scholar
[2]Gumbel, E. J., Statistics of extremes (Columbia University Press, New York, 1958).CrossRefGoogle Scholar
[3]Kemperman, J. H. B., The passage problem for a stationary Markov chain (University of Chicago Press, 1961).CrossRefGoogle Scholar
[4]Spitzer, F., Principles of Random Walk (Van Nostrand, Princeton, 1964).CrossRefGoogle Scholar