We study cosine and sine Fourier transforms defined by F(t):= (2/π) 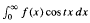and 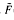(t):= (2/π), 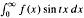where f is L1-integrable over[0, ∞]. We also assume than F 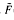are locally absolutely continuous over [0, ∞). In particular, this is the case if both f(x) and xf(x) are (L1-integrable over [0, ∞). Motivated by the inversion formulas, we consider the partial integras Sν (f, x):= 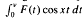and 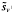ν(f, x):= 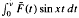, the modified partial integrals uν (f, x):= sν(f, x) - F(ν)(sin νx)/x and ũν(f, x):= 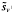ν(f, x) + 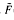(ν) (cos νx)/x, where ν > 0. We give necessary and sufficient conditions for(L1 [0, ∞)-convergence of uν (f) and ũν (f) as well as for the L1 [0, X]-convergence of sν (f) and 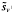ν(f) to f as ν← ∞, where 0 < X < ∞ is fixed. On the other hand, in certain cases we conclude that sν(f) and 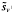ν(f) cannot belong to (L1 [0,∞). Conequently, it makes no sense to speak of their (L1 [0, ∞)-convergence as ν ← ∞.

As an intermediate tool, we use the Cesàro means of Fourier transforms. Then we prove Tauberian type results and apply Sidon type inequalities in order to obtain Tauberian conditions of Hardy-Karamata kind.

We extend these results to the complex Fourier transform defined by G(t):= 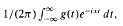, where g is L1- integrable over (−∞, ∞).