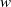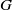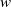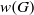Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KHUKHRO, E. I.
and
SHUMYATSKY, P.
2014.
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS.
Journal of the Australian Mathematical Society,
Vol. 97,
Issue. 3,
p.
343.
Detomi, Eloisa
Morigi, Marta
and
Shumyatsky, Pavel
2014.
Bounding the exponent of a verbal subgroup.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 193,
Issue. 5,
p.
1431.
ACCIARRI, CRISTINA
SHUMYATSKY, PAVEL
and
THILLAISUNDARAM, ANITHA
2014.
CONCISENESS OF COPRIME COMMUTATORS IN FINITE GROUPS.
Bulletin of the Australian Mathematical Society,
Vol. 89,
Issue. 2,
p.
252.
Khukhro, E. I.
and
Shumyatsky, P.
2015.
Nonsoluble and non-p-soluble length of finite groups.
Israel Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
507.
Detomi, Eloisa
Morigi, Marta
and
Shumyatsky, Pavel
2015.
On countable coverings of word values in profinite groups.
Journal of Pure and Applied Algebra,
Vol. 219,
Issue. 4,
p.
1020.
CONTRERAS–ROJAS, Y.
and
SHUMYATSKY, PAVEL
2015.
Nonsoluble length of finite groups with commutators of small order.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 158,
Issue. 3,
p.
487.
Khukhro, E. I.
and
Shumyatsky, P.
2021.
Compact groups in which all elements have countable right Engel sinks.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 151,
Issue. 6,
p.
1790.
Khukhro, E. I.
and
Shumyatsky, P.
2021.
Compact groups with countable Engel sinks.
Bulletin of Mathematical Sciences,
Vol. 11,
Issue. 03,
DETOMI, ELOISA
MORIGI, MARTA
and
SHUMYATSKY, PAVEL
2022.
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP.
Journal of the Australian Mathematical Society,
Vol. 113,
Issue. 2,
p.
145.
Khukhro, E. I.
and
Shumyatsky, P.
2023.
Strong conciseness of Engel words in profinite groups.
Mathematische Nachrichten,
Vol. 296,
Issue. 6,
p.
2404.